Cho 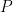 và
và 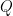 là hai số nguyên lẻ nguyên tố cùng nhau thỏa mãn
là hai số nguyên lẻ nguyên tố cùng nhau thỏa mãn  Dãy Lucas
Dãy Lucas 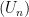 và dãy Lucas đồng hành
và dãy Lucas đồng hành 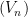 với tham số
với tham số 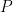 và
và 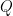 được xác định như sau:
được xác định như sau: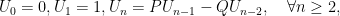 và
và 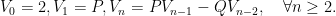 Khi
Khi  và
và 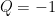 ta có
ta có 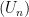 là dãy số Fibonacci. Vào quãng năm 1996, Paulo Ribenboim và Wayne L. McDaniel đã chứng minh được kết quả:
là dãy số Fibonacci. Vào quãng năm 1996, Paulo Ribenboim và Wayne L. McDaniel đã chứng minh được kết quả:
Định lí. Nếu  là số tự nhiên sao cho một trong bốn số
là số tự nhiên sao cho một trong bốn số 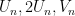 và
và  là số chính phương thì
là số chính phương thì 
Phương pháp của họ như sau. Chẳng hạn giả sử 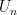 là số một chính phương, khi đó với mỗi số nguyên dương lẻ
là số một chính phương, khi đó với mỗi số nguyên dương lẻ  nguyên tố cùng nhau với
nguyên tố cùng nhau với 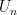 ta có ký hiệu Jacobi
ta có ký hiệu Jacobi  Với hầu hết
Với hầu hết 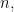 họ chọn được các modulo
họ chọn được các modulo 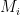 sao cho
sao cho 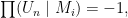 suy ra
suy ra 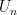 không phải là số chính phương, vô lý! Bạn đọc quan tâm có thể đọc trong bài:
không phải là số chính phương, vô lý! Bạn đọc quan tâm có thể đọc trong bài:
![\text{[P-W]}](https://s0.wp.com/latex.php?latex=%5Ctext%7B%5BP-W%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) Paulo Ribenboim and Wayne L. McDaniel, The Square Terms in Lucas Sequences. Journal of number theory 58, 104 -123 (1996).
Paulo Ribenboim and Wayne L. McDaniel, The Square Terms in Lucas Sequences. Journal of number theory 58, 104 -123 (1996).
Mục đích chính của tôi khi viết bài này chỉ là giới thiệu ![\text{[P-W]}](https://s0.wp.com/latex.php?latex=%5Ctext%7B%5BP-W%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) đến các đồng nghiệp và các học sinh. Trong đó có nhiều kết quả sơ cấp về dãy Lucas và dãy Lucas đồng hành, những dãy số mà chúng ta biết ít hơn so với dãy số Fibonacci. Tiếp theo tôi giới thiệu một lời giải cho bài toán sau, nó là ý b trong bài 4 của đề thi chọn đội tuyển IMO 2023.
đến các đồng nghiệp và các học sinh. Trong đó có nhiều kết quả sơ cấp về dãy Lucas và dãy Lucas đồng hành, những dãy số mà chúng ta biết ít hơn so với dãy số Fibonacci. Tiếp theo tôi giới thiệu một lời giải cho bài toán sau, nó là ý b trong bài 4 của đề thi chọn đội tuyển IMO 2023.
Bài toán (TST2023/4b). Cho hai số nguyên dương lẻ  và
và  nguyên tố cùng nhau. Xét dãy số
nguyên tố cùng nhau. Xét dãy số  xác định bởi
xác định bởi 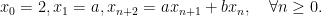 Chứng minh rằng không tồn tại bộ ba số nguyên dương
Chứng minh rằng không tồn tại bộ ba số nguyên dương  sao cho
sao cho  chẵn và
chẵn và  là số chính phương.
là số chính phương.
Lời giải. Với giả thiết của bài toán ta thấy  là dãy Lucas đồng hành với tham số
là dãy Lucas đồng hành với tham số  và
và  bởi vậy chúng ta có thể dùng các kết quả trong
bởi vậy chúng ta có thể dùng các kết quả trong ![\text{[P-W]}](https://s0.wp.com/latex.php?latex=%5Ctext%7B%5BP-W%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . Giả sử
. Giả sử  là một bộ ba số nguyên dương sao cho
là một bộ ba số nguyên dương sao cho  chẵn và
chẵn và  là số chính phương. Khi đó
là số chính phương. Khi đó  và
và  suy ra theo (9) trong
suy ra theo (9) trong ![\text{[P-W]}](https://s0.wp.com/latex.php?latex=%5Ctext%7B%5BP-W%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) (trang 107) ta có
(trang 107) ta có  và
và 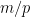 là các số nguyên dương lẻ. Do đó cấp
là các số nguyên dương lẻ. Do đó cấp  adic của
adic của  và
và  bằng nhau, để ý thêm
bằng nhau, để ý thêm  chẵn ta có
chẵn ta có  và
và  đều chẵn. Bây giờ theo bổ đề 1 trong
đều chẵn. Bây giờ theo bổ đề 1 trong ![\text{[P-W]}](https://s0.wp.com/latex.php?latex=%5Ctext%7B%5BP-W%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) ta có
ta có 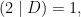 điều này không thể xảy ra vì
điều này không thể xảy ra vì 
Bài toán được giải.
—
Vậy tôi giải được bài toán này nhờ tôi biết nhiều, chứ không cần điều gì đặc biệt. Có đúng không các bạn học sinh? 🙂
—
18/04/2023: Anh Nguyễn Xuân Thọ (Đại học Bách Khoa) cho tôi biết là kết quả TST2023/4b này đã có trong Colloquium Mathematicum, Vol. 130, No. 1, 2013.
Một điểm không phù hợp nữa của bài toán này là đoạn đặc trưng các cặp 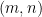 sao cho
sao cho  đã có trong đề thi chọn HSG QG năm 2018, cụ thể là Bài 6.
đã có trong đề thi chọn HSG QG năm 2018, cụ thể là Bài 6.




