IMO 2024: Problems and results

Ngày thi thứ nhất (16/7/2024)

Bài 1. https://artofproblemsolving.com/community/c6h3358923

Tìm tất cả các số thực $\alpha$ sao cho với mỗi số nguyên dương $n$ , số

$[\alpha]+[2\alpha]+\cdots+[n\alpha]$

chia hết cho $n$ .

Bài 2. https://artofproblemsolving.com/community/c6h3358926

Tìm tất cả các cặp số nguyên dương $(a,b)$ sao cho tồn tại các số nguyên dương $g$ và $N$ thỏa mãn

$\gcd (a^n+b,b^n+a)=g$

với mọi số nguyên $n\geq N$ .

Bài 3. https://artofproblemsolving.com/community/c6h3358932

Cho dãy vô hạn các số nguyên dương $(a_n)_{n\geq 1}$ và số nguyên dương $N$ . Giả sử với mọi số nguyên $n>N$ , $a_n$ bằng số lần xuất hiện của $a_{n-1}$ trong dãy số $a_1$ , $a_2$ , $\ldots$ , $a_{n-1}$ . Chứng minh rằng một trong hai dãy số $(a_{2n-1})_{n\geq 1}$ và $(a_{2n})_{n\geq 1}$ là tuần hoàn kể từ lúc nào đó.

Ngày thi thứ hai (17/7/2024)

Bài 4. https://artofproblemsolving.com/community/c6h3359767

Cho $ABC$ là một tam giác với $AB < AC < BC$ . Gọi tâm đường tròn nội tiếp và đường tròn nội tiếp của tam giác $ABC$ lần lượt là $I$ và $\omega$ . Gọi $X$ là điểm trên đường thẳng $BC$ , khác $C$ , sao cho đường thẳng qua $X$ song song với $AC$ tiếp xúc với $\omega$ . Tương tự, gọi $Y$ là điểm trên đường thẳng $BC$ , khác $B$ , sao cho đường thẳng qua $Y$ song song với $AB$ tiếp xúc với $\omega$ . Đường thẳng $AI$ cắt lại đường tròn ngoại tiếp tam giác $ABC$ tại $P$ . Gọi $K$ và $L$ lần lượt là trung điểm của $AC$ và $AB$ . Chứng minh rằng $\angle KIL + \angle YPX = 180^{\circ}$ .

Bài 5. https://artofproblemsolving.com/community/c6h3359777

Ốc sên Turbo chơi trò chơi sau trên một bảng ô vuông cỡ $2024\times 2023$ . Trong $2022$ ô vuông con nào đó, có các con quỷ nấp ở đó. Ban đầu, Turbo không biết ô nào có quỷ, nhưng nó biết rằng trên mỗi hàng có đúng một con quỷ, trừ hàng đầu tiên và hàng cuối cùng, và trên mỗi cột có không quá một con quỷ.

Turbo thực hiện một dãy các phép thử để tìm cách đi từ hàng đầu đến hàng cuối của bảng. Tại mỗi lần thử, nó được quyền chọn một ô bất kỳ trên hàng đầu để xuất phát, sau đó liên tục di chuyển giữa các ô, mỗi bước từ một ô sang một ô có chung cạnh với ô mà nó đang đứng (nó được phép đến các ô đã từng đi qua). Nếu nó tới một ô có quỷ thì lần thử này dừng lại và nó được đưa trở lại hàng đầu để thực hiện một lần thử khác. Những con quỷ không di chuyển, và Turbo nhớ mỗi ô mà nó ghé qua có quỷ hay không. Nếu nó tới được một ô bất kỳ trên hàng cuối thì trò chơi kết thúc.

Xác định giá trị nhỏ nhất của $n$ sao cho Turbo luôn có chiến lược đảm bảo tới được hàng cuối cùng sau không quá $n$ lần thử, cho dù các con quỷ có nấp ở đâu.

Bài 6. https://artofproblemsolving.com/community/c6h3359771

Một hàm số $f:\mathbb{Q}\to\mathbb{Q}$ được gọi là đẹp nếu với mỗi số hữu tỷ $x$ và $y$ , $f(x+f(y))=f(x)+y$ hoặc $f(f(x)+y)=x+f(y)$ . Chứng minh rằng tồn tại số nguyên $c$ sao cho với mọi hàm số đẹp $f$ , có không quá $c$ số hữu tỷ có dạng $f(r)+f(-r)$ , với số hữu tỷ $r$ nào đó. Tìm giá trị nhỏ nhất của các số $c$ có tính chất này.

Ban tổ chức quyết định điểm xếp giải như sau:

HCV: $\geq 29$ , HCB: $\geq 22$ , HCĐ: $\geq 16$ .

Đội tuyển Việt Nam được 2 HCB và 3 HCĐ. Đội đứng thứ 33 về tổng điểm.

Top 10 đội có điểm cao nhất. Đội tuyển Trung Quốc đứng thứ hai, sau nhiều năm đứng thứ nhất.

Top 10 thí sinh có điểm cao nhất. Haojia Shi lần thứ hai đạt 42/42 điểm. 🙂

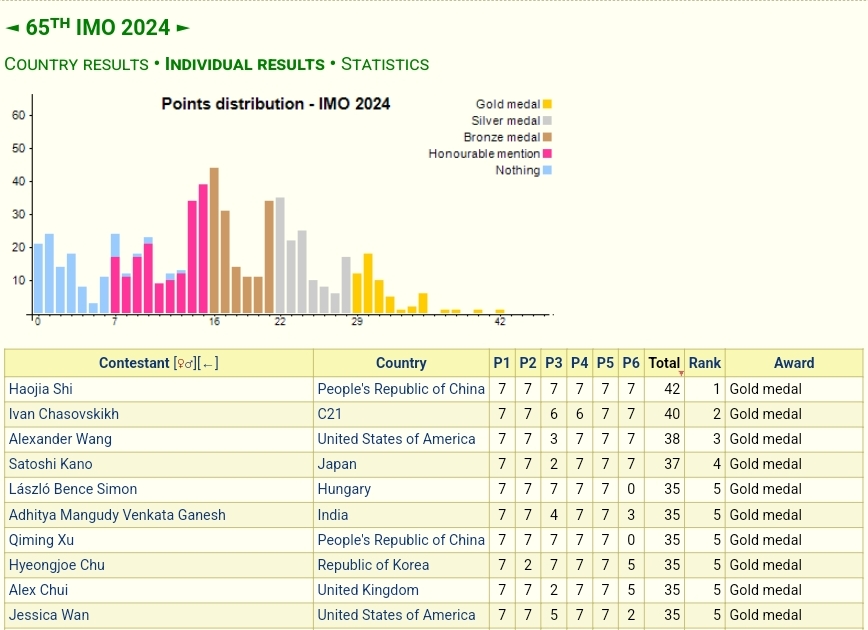
Nguồn ảnh: https://www.imo-official.org/

Algebraic number

Các em học sinh hãy chứng minh các khẳng định trong bài ngắn dưới đây. Tài liệu tham khảo là

[1] https://nttuan.org/2018/08/25/poly03/

[2] https://nttuan.org/2009/01/11/poly02/

[3] https://nttuan.org/2021/04/30/sqrt/

Một số phức $\alpha$ được gọi là một số đại số nếu có đa thức $f(x)$ khác đa thức không có hệ số trong $\mathbb{Q}$ nhận $\alpha$ làm nghiệm. Một số đại số được gọi là số nguyên đại số nếu nó là nghiệm của một đa thức có hệ số nguyên với hệ số cao nhất bằng $1$ .

$\sqrt[3]{2}$ và $i$ là các số đại số. Số $\frac{1}{2}$ là một số đại số nhưng không phải số nguyên đại số. Những số phức không phải là số đại số sẽ được gọi là các số siêu việt. Người ta chứng minh được $e$ và $\pi$ là các số siêu việt.

Cho một số đại số $\alpha$ . Đa thức tối tiểu của $\alpha$ là đa thức khác không $f(x)\in\mathbb{Q}[x]$ có bậc nhỏ nhất thỏa mãn

hệ số cao nhất của $f$ bằng $1$ , và
$\alpha$ là một nghiệm của $f$ .

Định lí 1. Đa thức tối tiểu là tồn tại và duy nhất với mỗi số đại số.

Định lí 2. Cho số đại số $\alpha$ . Khi đó

Đa thức tối tiểu của $\alpha$ là bất khả quy trên $\mathbb{Q}$ .
Nếu $g\in\mathbb{Q}[x]$ thì $\alpha$ là nghiệm của $g$ khi và chỉ khi $g$ chia hết cho đa thức tối tiểu của $\alpha$ .
Nếu đa thức tối tiểu của $\alpha$ có bậc $n$ thì với mỗi đa thức $f$ với hệ số hữu tỷ, tồn tại đa thức $g$ có bậc bé hơn $n$ với hệ số hữu tỷ sao cho $f(\alpha)=g(\alpha)$ .

Bài 1. Chứng minh rằng $\sqrt{2}+\sqrt{3}$ là một số đại số và tìm đa thức tối tiểu của nó.

Bài 2. Cho $p(x)$ là một đa thức với hệ số nguyên thỏa mãn $p(\sqrt{2}+\sqrt{3})=0$ . Chứng minh rằng $p(\sqrt{2}-\sqrt{3})=0$ .

Định lí 3. Nếu $\alpha$ và $\beta$ là các số đại số (nguyên đại số) thì $\alpha\pm\beta$ và $\alpha\beta$ cũng là các số đại số (nguyên đại số). Nếu $\alpha\not=0$ là một số đại số thì $1/\alpha$ cũng là một số đại số.

Khẳng định thứ hai không đúng đối với các số nguyên đại số.

Bài 3. Số $\sqrt {1001^2 + 1} + \sqrt {1002^2 + 1} + \cdots + \sqrt {2000^2 + 1}$ có phải là số hữu tỷ hay không?

Characters of finite Abelian groups

Cho $G$ là một nhóm giao hoán hữu hạn (với phép toán nhân). Một đặc trưng của $G$ là một đồng cấu từ $G$ đến nhóm nhân $U$ các số phức có mô đun bằng $1$ . Với một đặc trưng $\chi: G\to U$ , ta có

các giá trị của $\chi$ là các căn bậc $\mid G\mid$ của đơn vị.
$(\chi (g))^{-1}=\overline{\chi (g)},\quad\forall g\in G$ .

Ánh xạ $\chi_0:G\to U$ xác định bởi $\chi (g)=1,\quad\forall g\in G,$ là một đặc trưng của $G$ . Nó được gọi là đặc trưng tầm thường, các đặc trưng khác của $G$ được gọi là đặc trưng không tầm thường.

Cho $\chi:G\to U$ là một đặc trưng của $G$ . Khi đó ánh xạ $\overline{\chi}:G\to U$ xác định bởi $\overline{\chi} (g)=\overline{\chi (g)},\quad\forall g\in G,$ cũng là một đặc trưng của $G$ . Nó được gọi là đặc trưng liên hợp của $\chi$ .

Với hai đặc trưng $\chi_1$ và $\chi_2$ của $G$ , ta có thể định nghĩa đặc trưng tích của chúng, ký hiệu $\chi_1\chi_2$ , bởi

$(\chi_1\chi_2) (g)=\chi_1(g)\chi_2(g),\quad\forall g\in G$ (dễ kiểm tra thấy đây là một đặc trưng của $G$ ). Với phép toán này thì tập hợp $\widehat{G}$ gồm tất cả các đặc trưng của $G$ trở thành một nhóm giao hoán, nhóm đối ngẫu của $G$ . Nhóm này là hữu hạn vì các giá trị của đặc trưng là các căn bậc $\mid G\mid$ của đơn vị.

Cho số nguyên dương $n$ và nhóm cyclic $G$ có cấp bằng $n$ . Gọi $g$ là một phần tử sinh của $G$ . Khi đó $\mid \widehat{G}\mid=n$ và $\widehat{G}=\{\chi_0,\chi_1,\ldots,\chi_{n-1}\},$ ở đây đặc trưng $\chi_j$ xác định bởi $\chi_j(g^k)=\exp \left(i\cdot \frac{2\pi j k}{n}\right)$ với mọi $k=0$ , $1,\ldots$ , $n-1$ .

Định lí 1. Cho $H$ một nhóm con của $G$ và $\chi$ là một đặc trưng của $H$ . Khi đó $\chi$ có thể mở rộng thành một đặc trưng của $G$ .

Chứng minh. Ta chỉ cần xét trường hợp $G$ là nhóm con sinh bởi $H\cup \{a\}$ , trong đó $a\in G\setminus H$ . Gọi $n$ là số nguyên dương nhỏ nhất sao cho $a^n\in H$ , và $b$ là một căn bậc $n$ của $\chi (a^n)$ . Mọi phần tử $g$ của $G$ đều viết được một cách duy nhất dưới dạng $g=a^ih$ , với $h\in H$ và $0\leq i<n$ . Ánh xạ $\chi_1:G\to U$ xác định bởi $\chi_1(g)=\chi_1(a^ih)=b^i\chi (h)$ là một đặc trưng của $G$ mở rộng $\chi$ . $\Box$

Continue reading →

Erdos–Ginzburg–Ziv theorem

Định lí Erdos–Ginzburg–Ziv. Cho số nguyên dương $n.$ Khi đó trong mỗi $2n-1$ số nguyên, tồn tại $n$ số có tổng chia hết cho $n.$

Chứng minh. Trước tiên ta thấy khẳng định đúng với $n=1,$ và nếu khẳng định đúng với $x>1$ và $y>1$ thì nó cũng đúng với $xy.$ Thật vậy, giả sử $a_1,a_2,\ldots,a_{2xy-1}$ là các số nguyên bất kỳ. Trước tiên, vì $2xy-1>2y-1$ nên trong các số đã cho ta có thể chọn $y$ số $a_{1j}$ sao cho $\displaystyle a_{11}+a_{12}+\cdots +a_{1y}\equiv 0\pmod{y},$ sau bước này ta còn $2xy-1-y=(2x-1)y-1>2y-1$ số. Trong $(2x-1)y-1$ số đó ta chọn $y$ số $a_{2j}$ sao cho

$a_{21}+a_{22}+\cdots+a_{2y}\equiv 0\pmod{y},$ sau bước này ta còn $(2x-2)y-1$ số. Tiếp tục làm như vậy cuối cùng ta được $(2x-1)y$ số $a_{ij}$ thỏa mãn

$a_{i1}+a_{i2}+\cdots+a_{iy}\equiv 0\pmod{y},\quad \forall i=\overline{1,2x-1}.$ Vì khẳng định đúng với $n=x$ nên trong $2x-1$ số nguyên $\displaystyle\frac{1}{y}(a_{i1}+a_{i2}+\cdots+a_{iy}),$ tồn tại $x$ số, chẳng hạn $\displaystyle\frac{1}{y}(a_{i1}+a_{i2}+\cdots+a_{iy})$ với $i=1,$ $2,\ldots,$ $x$ , có tổng chia hết cho $x.$ Khi đó $xy$ số $a_{ij}$ với $(i,j)\in [x]\times [y]$ có tổng chia hết cho $xy,$ suy ra khẳng định đúng với $xy.$

Vậy ta chỉ cần chứng minh nó đúng với các số nguyên tố. Giả sử $n=p$ là một số nguyên tố và $a_0,$ $a_1,\ldots,$ $a_{2p-2}$ là các số nguyên bất kỳ. Ta cần chỉ ra có $p$ số trong các số đã cho có tổng chia hết cho $p.$ Với mỗi số nguyên $\alpha,$ ký hiệu $(\alpha)_p$ là số dư khi chia $\alpha$ cho $p.$ Không mất tính tổng quát, giả sử $\{(a_i)_p\}$ là một dãy không giảm. Nếu tồn tại $i\in [p-1]$ sao cho $(a_i)_p=(a_{i+p-1})_p$ thì

$(a_i)_p=(a_{i+1})_p=\cdots =(a_{i+p-1})_p\Rightarrow \sum_{j=i}^{i+p-1}a_j\equiv 0\pmod{p},$ nếu không, xét $p-1$ tập $A_i=\{a_i,a_{i+p-1}\}$ và dùng hệ quả trong [1] ta có