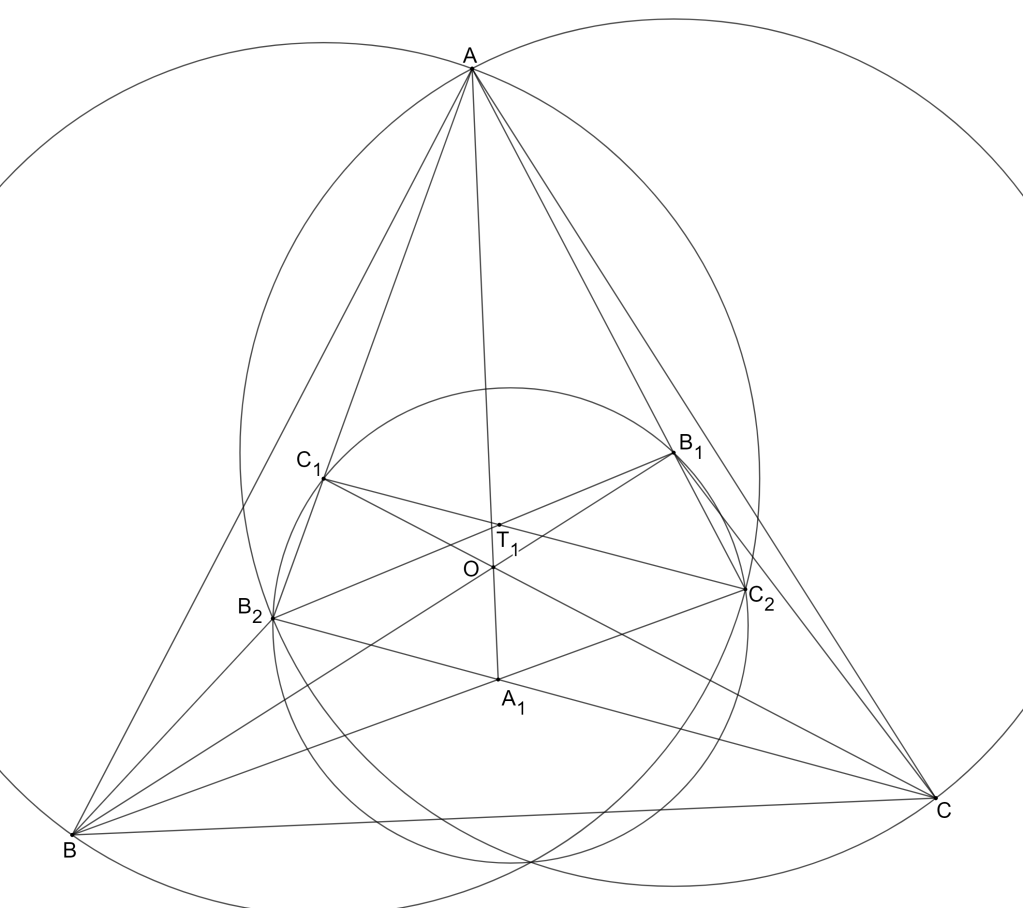IMO2011/6: Miquel circles and Steiner line

Sau khi giải xong bài IMO2023/6 ([1]) tôi vào topic thảo luận về bài toán đó trên AoPS ([2]) để tham khảo các lời giải khác. Tôi thấy parmenides51 bình luận rằng trong lịch sử IMO thì bài này là bài khó thứ nhì trong các bài hình học, bài khó nhất là bài IMO2011/6. Do tò mò tôi vào trang chủ của IMO ([3]) xem bài toán đó thế nào? Dưới đây là đề bài:

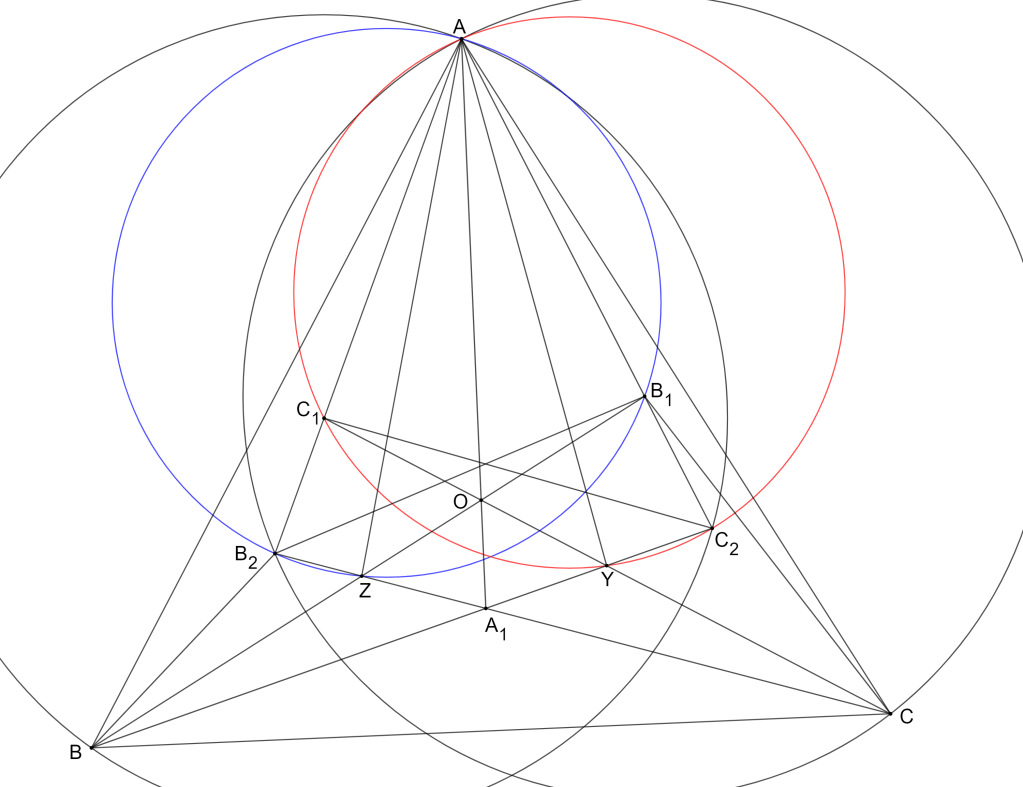
IMO2011/6. Cho tam giác nhọn $ABC$ với đường tròn ngoại tiếp $\Gamma$ . Giả sử $l$ là một tiếp tuyến nào đó của $\Gamma$ . Gọi $l_a$ , $l_b$ , và $l_c$ là những đường thẳng nhận được từ $l$ bằng cách lấy đối xứng qua $BC$ , $CA$ , và $AB$ , tương ứng. Chứng minh rằng đường tròn ngoại tiếp của tam giác tạo bởi ba đường thẳng $l_a$ , $l_b$ , và $l_c$ tiếp xúc với $\Gamma$ .

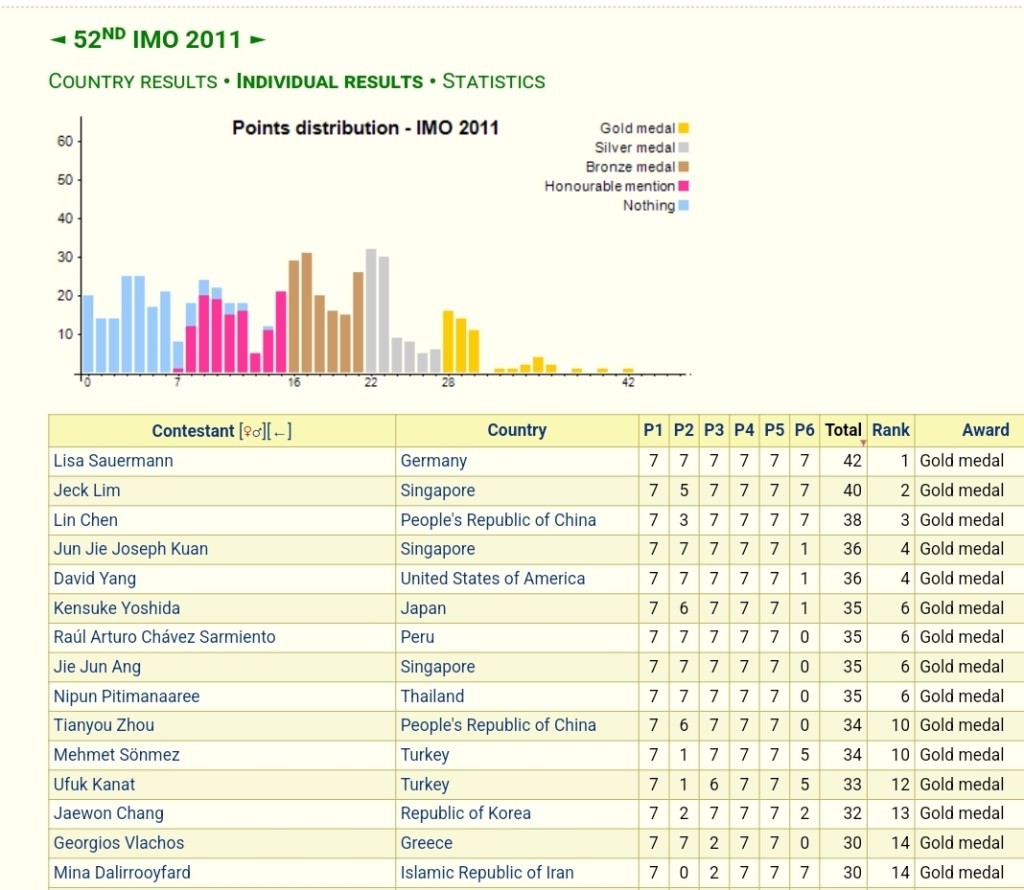
Trong điều kiện phòng thi thì thống kê chứng tỏ đây là bài hình học khó nhất trong lịch sử IMO! Ảnh sau tôi lấy từ [3], chỉ có $4$ thí sinh làm được bài toán này. Một bài toán rất rất khó!

Chỉ có 4 thí sinh làm được bài IMO2011/6.

Tôi thích bài IMO2023/6 bởi nó khá lạ so với các bài toán hình thường làm, bài IMO2011/6 này hấp dẫn tôi bởi sự giản dị. Không thể tin được là có kết quả này! Tôi quyết định lập một topic trên blog của tôi để làm việc với bài toán mỗi khi có thời gian (công việc chính của tôi là dạy đại số và số học cho các học sinh Chuyên toán bậc THPT), nó có thể lấy của tôi vài ngày hay nhiều tuần. Khi tôi đang gõ dòng này thì topic đang ở trạng thái ĐỢI, giải được bài toán tôi sẽ bấm nút CÔNG BỐ. Ở mỗi thời điểm, có được kết quả mới nào tôi sẽ sửa vào đây. Lời giải được viết theo hình vẽ trong bài, các trường hợp khác được bỏ qua.

Continue reading →

IMO2023/6: Coaxal circles

Trong bài này chúng tôi sẽ giới thiệu một lời giải của bài 6 trong kỳ thi Olympic Toán quốc tế năm 2023 (IMO 2023). Đề thi đã có ở đây https://nttuan.org/2023/07/08/imo2023-problems/

Chúng tôi trình bày lời giải theo hình vẽ tương ứng, các tình huống khác được bỏ qua. Đầu tiên ta phải hiểu thêm về đẳng thức giữa các góc trong đề bài, bởi vì ta không thể vẽ các điểm $A_1$ , $B_1$ và $C_1$ một cách tùy tiện và hy vọng giải được bài toán. Gọi $O$ là tâm của tam giác đều $ABC$ . Từ giả thiết ta có $\sum (180^{\circ}-2\widehat{A_1BC})=480^{\circ},$ suy ra $\widehat{A_1CB}+\widehat{B_1CA}=\widehat{B_2AA_1}.\quad (*)$ Đến đây ta ký hiệu $W$ là ảnh của $B_1$ qua phép quay tâm $C$ góc $+60^{\circ},$ cùng phép quay biến $A$ thành $B$ .

Khi đó $W$ thuộc tia $AA_1$ và $(*)$ được viết lại dưới dạng $\widehat{B_2CW}=\widehat{B_2AW}.$ Do đó bốn điểm $B_2$ , $A$ , $C$ , và $W$ cùng nằm trên một đường tròn. Đường tròn này có tâm là $B_1$ vì $CB_1=CW=B_1W=B_1A.$
Như vậy ta đã chứng minh được kết quả sau:

$(\alpha)$ : $B_1$ là tâm của $(CAB_2)$ , $C_1$ là tâm của $(ABC_2)$ , và $A_1$ là tâm của $(BCA_2)$ .

Tiếp theo, ta sẽ tìm hai điểm khác nhau có cùng phương tích đối với cả ba đường tròn ngoại tiếp các tam giác $AA_1A_2, BB_1B_2$ và $CC_1C_2$ . Làm được điều này là ta giải được bài toán. Mới đầu chúng tôi định giải nghĩa một cách hình học hai giao điểm của ba đường tròn, hay là chứng minh tâm của ba đường tròn thẳng hàng. Nhưng không thành công!

$(\beta)$ : Ba đường thẳng $A_1A_2$ , $B_1B_2$ , và $C_1C_2$ đồng quy. Nếu ký hiệu $T_1$ là điểm thuộc cả ba đường thẳng, thì $T_1$ có cùng phương tích đối với $(AA_1A_2)$ , $(BB_1B_2)$ , và $(CC_1C_2)$ .

Theo $(\alpha)$ , các tam giác $C_1C_2A$ và $B_1B_2A$ là các tam giác cân, suy ra
$\widehat{B_1B_2C_1}=\widehat{B_2AC_2}=\widehat{B_1C_2C_1}.$ Do đó tứ giác $B_1C_1B_2C_2$ là một tứ giác nội tiếp, tương tự ta cũng có hai tứ giác nội tiếp khác. Theo định lí về tâm đẳng phương của ba đường tròn ta có $(\beta)$ .

$(\gamma)$ : $\widehat{BAB_2}+\widehat{BB_1B_2}=\widehat{CAC_2}+\widehat{CC_1C_2}.$

Gọi $Z$ là giao điểm của $BB_1$ với $CB_2$ , và $Y$ là giao điểm của $BC_2$ với $CC_1$ . Ta có $\widehat{B_1ZC}=\widehat{A_1CB}+30^{\circ}=30^{\circ}-\widehat{BAC_1}-\widehat{B_1AC}+30^{\circ}=\widehat{B_2AB_1},$ nên tứ giác $AB_2ZB_1$ là một tứ giác nội tiếp. Chứng minh tương tự ta cũng có tứ giác $AC_1YC_2$ nội tiếp. Từ hai tứ giác nội tiếp này ta thấy vế trái và vế phải trong $(\gamma)$ lần lượt bằng $\widehat{BAZ}$ và $\widehat{CAY},$ chỉ việc để ý thêm rằng $Y$ và $Z$ đối xứng với nhau qua $AO$ là ta có $(\gamma)$ .

Continue reading →

IMO 2023: Problems and results

Bài viết này có hai phần: Phần thứ nhất là đề thi IMO 2023, phần thứ hai là kết qủa của kỳ thi.

Ngày thi thứ nhất, 8/7/2023

Bài 1. https://artofproblemsolving.com/community/c6h3106752

Tìm tất cả các hợp số $n$ có tính chất: nếu $d_1, d_2, \ldots, d_k$ là tất cả ước dương của $n$ với $1=d_1<d_2<\cdots<d_k=n$ , thì $d_i$ chia hết $d_{i+1}+d_{i+2}$ với mọi $1 \leqslant i \leqslant k-2$ .

Bài 2. https://artofproblemsolving.com/community/c6h3106748

Cho tam giác nhọn $ABC$ với $AB<AC$ . Gọi $S$ là điểm chính giữa của cung $BC$ chứa $A$ của $(ABC)$ . Đường thẳng qua $A$ vuông góc với $BC$ cắt $BS$ tại $D$ và cắt lại $(ABC)$ tại $E$ . Đường thẳng qua $D$ song song với $BC$ cắt $BE$ tại $L$ . $(BDL)$ cắt lại $(ABC)$ tại $P$ . Chứng minh rằng tiếp tuyến của $(BDL)$ tại $P$ cắt $BS$ trên phân giác của góc $BAC$ .

Bài 3. https://artofproblemsolving.com/community/c6h3106754

Với số nguyên $k>1,$ tìm tất cả các dãy vô hạn số nguyên dương $a_1,a_2,\ldots$ sao cho tồn tại đa thức $P$ với hệ số nguyên không âm có dạng $P(x)=x^k+c_{k-1}x^{k-1}+\cdots+c_1x+c_0$ để $P(a_n)=a_{n+1}a_{n+2}\cdots a_{n+k}$ với mọi số nguyên dương $n.$

Ngày thi thứ hai, 9/7/2023

Bài 4. https://artofproblemsolving.com/community/c6h3107339

Cho $2023$ số thực dương $x_1,x_2,\ldots,x_{2023}$ đôi một khác nhau thỏa mãn

$\displaystyle a_n=\sqrt{\left(x_1+x_2+\cdots+x_n\right)\left(\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}\right)}$

là số nguyên với mọi $n=1,2,\ldots,2023$ . Chứng minh rằng $a_{2023}\geq 3034$ .

Bài 5. https://artofproblemsolving.com/community/c6h3107350

Cho $n$ là một số nguyên dương. Một tam giác Nhật Bản gồm $1+2+\cdots+n$ hình tròn được xếp thành một hình tam giác đều sao cho với mỗi $i = 1, 2, ..., n$ , hàng thứ $i$ có đúng $i$ hình tròn và trên hàng đó có đúng một hình tròn được tô màu đỏ. Một đường đi ninja trong một tam giác Nhật Bản là một dãy gồm $n$ hình tròn nhận được bằng cách xuất phát từ hàng trên cùng, đi lần lượt từ một hình tròn xuống một trong hai hình tròn ngay dưới nó, và kết thúc tại hàng dưới cùng. Trong hình vẽ là một tam giác Nhật Bản với $n = 6$ và một đường đi ninja có chứa hai hình tròn màu đỏ.

Như một hàm số của $n$ , tìm giá trị lớn nhất của $k$ sao cho trong mỗi tam giác Nhật Bản luôn có một đường đi ninja chứa ít nhất $k$ hình tròn màu đỏ.

Bài 6. https://artofproblemsolving.com/community/c6h3107345

Cho $ABC$ là một tam giác đều. Gọi $A_1,B_1,C_1$ là các điểm nằm trong tam giác $ABC$ sao cho $BA_1=A_1C$ , $CB_1=B_1A$ , $AC_1=C_1B$ , và

$\angle BA_1C+\angle CB_1A+\angle AC_1B=480^\circ.$

Giả sử $BC_1$ và $CB_1$ cắt nhau tại $A_2,$ $CA_1$ và $AC_1$ cắt nhau tại $B_2$ , $AB_1$ và $BA_1$ cắt nhau tại $C_2.$ Chứng minh rằng nếu tam giác $A_1B_1C_1$ là tam giác không cân thì ba đường tròn ngoại tiếp các tam giác $AA_1A_2, BB_1B_2$ và $CC_1C_2$ đi qua hai điểm chung.