Trong bài này chúng tôi sẽ trình bày quan hệ chia hết trên tập các số nguyên. Bài viết là tài liệu tự học của các học sinh lớp 10 đang học tại T’s Lab, nhưng các bạn học sinh lớp 8 hoặc 9 xuất sắc có thể hiểu được toàn bài mà không gặp khó khăn nào. Nhiều chứng minh trong bài dùng tính chất sau của tập các số nguyên không âm.
Mỗi tập khác rỗng gồm các số nguyên không âm đều có phần tử nhỏ nhất.
Đầu tiên chúng ta đến với định lí nền tảng của toàn bài.
Định lí 1 (Thuật toán chia). Cho hai số nguyên  và
và  với
với  Khi đó tồn tại đúng một cặp số nguyên
Khi đó tồn tại đúng một cặp số nguyên  thỏa mãn
thỏa mãn
 và
và  . Hai số
. Hai số 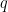 và
và  lần lượt được gọi là thương và dư trong phép chia
lần lượt được gọi là thương và dư trong phép chia  cho
cho  .
.
Chứng minh. Gọi  là tập hợp tất cả các số nguyên không âm có dạng
là tập hợp tất cả các số nguyên không âm có dạng  , với một số nguyên
, với một số nguyên  . Ta thấy
. Ta thấy  khác rỗng nên nó có phần tử nhỏ nhất, ký hiệu là
khác rỗng nên nó có phần tử nhỏ nhất, ký hiệu là  . Từ định nghĩa của
. Từ định nghĩa của  , ta có thể viết
, ta có thể viết  trong đó
trong đó 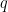 là một số nguyên. Nếu
là một số nguyên. Nếu  thì
thì  là một phần tử nhỏ hơn
là một phần tử nhỏ hơn  của
của  , vô lý, do đó
, vô lý, do đó  . Bây giờ giả sử
. Bây giờ giả sử  và
và  là hai cặp có tính chất nói đến trong định lí. Khi đó
là hai cặp có tính chất nói đến trong định lí. Khi đó  và
và  . Từ đây ta có
. Từ đây ta có  để ý thêm
để ý thêm  , ta thu được
, ta thu được  Suy ra
Suy ra  , và
, và  .
. 
Ví dụ 1. Từ định lí 1 ta thấy mọi số nguyên đều có thể viết được dưới dạng 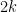 hoặc
hoặc  với một số nguyên
với một số nguyên 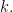 Tương tự, mọi số nguyên đều có thể viết được dưới dạng
Tương tự, mọi số nguyên đều có thể viết được dưới dạng 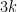 ,
,  , hoặc
, hoặc  với một số nguyên
với một số nguyên 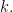

Định nghĩa 1. Cho hai số nguyên  và
và  với
với  khác
khác 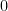 . Khi đó
. Khi đó  được gọi là chia hết cho
được gọi là chia hết cho  , ký hiệu
, ký hiệu  , nếu tồn tại số nguyên
, nếu tồn tại số nguyên  sao cho
sao cho  . Ta viết
. Ta viết  khi
khi  không chia hết cho
không chia hết cho  .
.
Khi  , ta cũng nói
, ta cũng nói  là một ước của
là một ước của  , hay
, hay  là một bội của
là một bội của  . Ta có ngay lập tức các tính chất sau, chứng minh của chúng là bài tập cho bạn đọc.
. Ta có ngay lập tức các tính chất sau, chứng minh của chúng là bài tập cho bạn đọc.
Định lí 2. Với các số nguyên  ,
,  , và
, và  , ta có các tính chất sau:
, ta có các tính chất sau:
(1)  .
.
(2)  khi và chỉ khi
khi và chỉ khi  .
.
(3) Nếu 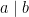 và
và  , thì
, thì  .
.
(4) Nếu 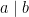 và
và  , thì
, thì 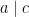 .
.
(5) 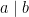 và
và  khi và chỉ khi
khi và chỉ khi  .
.
(6) Nếu 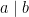 và
và  , thì
, thì  .
.
(7) Nếu 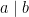 và
và 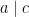 , thì
, thì  với các số nguyên bất kỳ
với các số nguyên bất kỳ  và
và 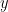 .
.
Ta xét một số ví dụ có sử dụng các tính chất này.
Ví dụ 2. Cho  ,
,  ,
,  , và
, và  là các số nguyên thỏa mãn
là các số nguyên thỏa mãn  . Chứng minh rằng ít nhất một bốn số đã cho không chia hết cho
. Chứng minh rằng ít nhất một bốn số đã cho không chia hết cho 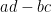 .
.
Lời giải. Giả sử ngược lại, khi đó cả bốn số  ,
,  ,
,  , và
, và  đều chia hết cho
đều chia hết cho 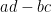 . Suy ra
. Suy ra  và
và  cùng chia hết cho
cùng chia hết cho  , do đó
, do đó  điều này không thể xảy ra vì
điều này không thể xảy ra vì  .
. 
Ví dụ 3. Tìm tất cả bộ ba số nguyên 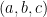 sao cho
sao cho  và
và  là một ước của
là một ước của 
Lời giải. Các bộ ba phải tìm là  và
và  . Giả sử
. Giả sử 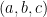 là một bộ ba thỏa mãn các yêu cầu của đề bài. Khi đó ba số
là một bộ ba thỏa mãn các yêu cầu của đề bài. Khi đó ba số  ,
,  và
và  có cùng tính chẵn-lẻ, do đó
có cùng tính chẵn-lẻ, do đó  suy ra
suy ra  Đến đây xét
Đến đây xét 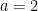 và
và 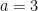 ta có câu trả lời.
ta có câu trả lời. 
Continue reading “Divisibility theory in the integers” →
là các số nguyên không đồng thời bằng
. Chứng minh rằng nếu
là các số nguyên dương đôi một khác nhau và không có ước chính phương lớn hơn
thì
.
, số ước nguyên tố của
, khẳng định: Tồn tại tổng
sao cho
là số nguyên khác
, ở đây
là các số nguyên dương đôi một khác nhau và không có ước chính phương khác
, tập các ước nguyên tố của
là tập con của tập các ước nguyên tố của
,
là các số nguyên, và
. Từ đó suy ra
.
ta chọn
.
ta chọn
khi
, chọn
nếu
.