Đây là bài thứ ba về đa thức của tôi, các bạn học sinh nên xem lại hai bài trước để học cho dễ dàng hơn. Như các bài trước, các bạn học sinh tự hoàn thiện các lời giải một cách chi tiết.
[1] https://nttuan.org/2023/06/30/poly01/
[2] https://nttuan.org/2023/08/11/poly02/
Mục đích của bài này là giới thiệu một số kết quả cơ bản về các đa thức với hệ số nguyên, chẳng hạn như định lí nghiệm hữu tỷ và tiêu chuẩn bất khả quy của Eisenstein.
Định lí 1 (Định lí nghiệm hữu tỷ). Cho số nguyên dương  và đa thức
và đa thức

có bậc bằng  với hệ số nguyên. Khi đó nếu
với hệ số nguyên. Khi đó nếu  là một nghiệm hữu tỷ khác không của
là một nghiệm hữu tỷ khác không của 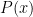 thỏa mãn
thỏa mãn  , thì
, thì  and
and  .
.
Chứng minh. Từ giả thiết ta có 
suy ra  và
và  . Nhưng
. Nhưng  và
và  nguyên tố cùng nhau, nên
nguyên tố cùng nhau, nên  và
và  .
. 
Theo định lí này, khi 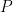 có hệ số cao nhất bằng
có hệ số cao nhất bằng 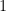 thì mọi nghiệm hữu tỷ của
thì mọi nghiệm hữu tỷ của 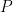 đều là số nguyên. Với một đa thức khác hằng với hệ số nguyên, từ định lí ta cũng thấy muốn tìm nghiệm hữu tỷ của đa thức ta chỉ cần tìm trong một tập hợp hữu hạn.
đều là số nguyên. Với một đa thức khác hằng với hệ số nguyên, từ định lí ta cũng thấy muốn tìm nghiệm hữu tỷ của đa thức ta chỉ cần tìm trong một tập hợp hữu hạn.
Ví dụ 1. Giả sử ta muốn tìm tất cả các nghiệm hữu tỷ của đa thức  Theo định lí, nghiệm hữu tỷ của
Theo định lí, nghiệm hữu tỷ của 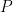 phải là nghiệm nguyên và nó bằng
phải là nghiệm nguyên và nó bằng 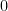 hoặc là ước của
hoặc là ước của 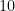 . Suy ra nghiệm hữu tỷ của
. Suy ra nghiệm hữu tỷ của 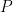 thuộc tập hợp
thuộc tập hợp  Kiểm tra trực tiếp ta thấy nghiệm hữu tỷ của đa thức là
Kiểm tra trực tiếp ta thấy nghiệm hữu tỷ của đa thức là  .
.
Định nghĩa 1. Một đa thức khác không với hệ số nguyên được gọi là nguyên bản nếu các hệ số của nó chỉ có ước dương chung là 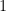 .
.
Định lí 2 (Bổ đề Gauss). Tích của hai đa thức nguyên bản là một đa thức nguyên bản.
Chứng minh. Giả sử  là tích của hai đa thức nguyên bản và
là tích của hai đa thức nguyên bản và  là một số nguyên tố chia hết mọi hệ số của
là một số nguyên tố chia hết mọi hệ số của  . Viết
. Viết  và
và  . Do
. Do  và
và  là nguyên bản nên ta có thể chọn các chỉ số
là nguyên bản nên ta có thể chọn các chỉ số 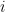 và
và 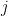 lớn nhất để
lớn nhất để  và
và  . Khi đó hệ số của
. Khi đó hệ số của  trong
trong  bằng
bằng  , số này không chia hết cho
, số này không chia hết cho  , vô lý.
, vô lý. 
Hệ quả. Cho 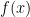 là một đa thức khác hằng với hệ số nguyên sao cho
là một đa thức khác hằng với hệ số nguyên sao cho  , ở đây
, ở đây  và
và 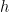 là các đa thức khác hằng với hệ số hữu tỷ. Khi đó
là các đa thức khác hằng với hệ số hữu tỷ. Khi đó  là tích của hai đa thức với hệ số nguyên có bậc bằng bậc của
là tích của hai đa thức với hệ số nguyên có bậc bằng bậc của  và
và 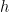 .
.
Chứng minh. Từ giả thiết ta có thể viết  , trong đó
, trong đó  và
và  là hai số nguyên dương nguyên tố cùng nhau, và
là hai số nguyên dương nguyên tố cùng nhau, và  là hai đa thức nguyên bản có bậc lần lượt bằng bậc của
là hai đa thức nguyên bản có bậc lần lượt bằng bậc của  ,
, 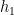 . Nếu
. Nếu  là một hệ số của
là một hệ số của  thì
thì  do
do  có hệ số nguyên, suy ra
có hệ số nguyên, suy ra  . Như vậy
. Như vậy  là số nguyên dương chia hết mọi hệ số của đa thức
là số nguyên dương chia hết mọi hệ số của đa thức  , là một đa thức nguyên bản theo bổ đề Gauss, suy ra
, là một đa thức nguyên bản theo bổ đề Gauss, suy ra 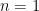 . Khi đó
. Khi đó  , đây là phân tích ta cần.
, đây là phân tích ta cần. 
Bằng quy nạp ta dễ dàng mở rộng kết quả trên cho nhiều hơn hai thừa số.
Định lí 3 (Tiêu chuẩn Eisenstein). Cho số nguyên dương  và đa thức
và đa thức  có bậc
có bậc  với hệ số nguyên. Giả sử có số nguyên tố
với hệ số nguyên. Giả sử có số nguyên tố  sao cho
sao cho 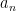 không chia hết cho
không chia hết cho  , các hệ số
, các hệ số  chia hết cho
chia hết cho  và
và 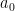 không chia hết cho
không chia hết cho  . Khi đó
. Khi đó  là đa thức bất khả quy trên
là đa thức bất khả quy trên 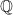 .
.
Chứng minh. Giả sử  không bất khả quy trên
không bất khả quy trên  Khi đó theo hệ quả trên, tồn tại các đa thức khác hằng với hệ số nguyên
Khi đó theo hệ quả trên, tồn tại các đa thức khác hằng với hệ số nguyên  và
và 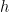 sao cho
sao cho  Viết
Viết  và
và  trong đó
trong đó  ,
,  là các số nguyên dương và
là các số nguyên dương và  Vì
Vì  chia hết cho
chia hết cho  nhưng không chia hết cho
nhưng không chia hết cho  nên
nên  hoặc
hoặc  và không xảy ra cả hai. Giả sử mà không làm mất tính tổng quát rằng
và không xảy ra cả hai. Giả sử mà không làm mất tính tổng quát rằng  và
và 
Nếu  chia hết cho
chia hết cho  thì bằng cách để ý đến hệ số của
thì bằng cách để ý đến hệ số của  trong hai vế của
trong hai vế của  ta có
ta có  cũng chia hết cho
cũng chia hết cho 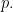 Vậy bằng quy nạp theo
Vậy bằng quy nạp theo 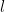 , ta có
, ta có  với mỗi
với mỗi  . Suy ra
. Suy ra  chia hết cho
chia hết cho  , vô lý.
, vô lý. 
Hệ quả. Với mỗi số nguyên tố  , đa thức
, đa thức  bất khả quy trên
bất khả quy trên 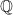 .
.
Chứng minh. Xét một số nguyên tố  . Ta có
. Ta có
 và khi
và khi  thì
thì  chia hết
chia hết  . Suy ra theo tiêu chuẩn Eisenstein, đa thức
. Suy ra theo tiêu chuẩn Eisenstein, đa thức  bất khả quy trên
bất khả quy trên 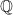 , do đó
, do đó  bất khả quy trên
bất khả quy trên 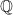 .
. 
Continue reading “Polynomials with integer coefficients” →