Tôi sẽ dịch một đoạn trong bài Leonard Euler’s Solution to the Konigsberg Bridge Problem của Teo Paoletti. Khi tình cờ gặp bài viết này tôi đã quyết định sử dụng nó làm bài mở đầu trong bài giảng về lý thuyết đồ thị của tôi.
Câu chuyện của chúng ta bắt đầu vào thế kỷ 18, tại thị trấn cổ kính Konigsberg, Phổ, bên bờ sông Pregel. Năm 1254, các hiệp sĩ Teutonic thành lập thành phố Konigsberg dưới sự lãnh đạo của Vua Bohemian Ottoker II sau cuộc thập tự chinh thứ hai chống lại quân Phổ. Vào thời Trung cổ, Konigsberg đã trở thành một thành phố và trung tâm thương mại rất quan trọng với vị trí chiến lược bên sông. Các tác phẩm nghệ thuật từ thế kỷ 18 cho thấy Konigsberg là một thành phố thịnh vượng, nơi các đội tàu cập bến Pregel, và hoạt động buôn bán của họ mang lại cuộc sống thoải mái cho cả thương nhân địa phương và gia đình họ. Nền kinh tế phát triển cho phép người dân thành phố xây dựng bảy cây cầu bắc qua sông, hầu hết trong số đó nối với đảo Kneiphof, vị trí của chúng có thể được thấy trong hình dưới đây.
Khi dòng sông chảy quanh Kneiphof và một hòn đảo khác, nó chia thành phố thành bốn vùng độc lập. Theo truyền thuyết, người dân Konigsberg thường dành những buổi chiều Chủ nhật để đi dạo quanh thành phố xinh đẹp của họ. Trong khi đi bộ, người dân thành phố quyết định tạo ra một trò chơi cho chính họ. Mục tiêu là nghĩ ra cách để có thể đi bộ quanh thành phố mà chỉ băng qua mỗi cây cầu đúng một lần. Mặc dù không ai ở Konigsberg có thể phát hiện ra một tuyến đường như vậy, nhưng họ vẫn không thể chứng minh được rằng điều đó là không thể. May mắn cho họ, Konigsberg không quá xa St. Petersburg, quê hương của nhà toán học nổi tiếng Leonard Euler.
Tại sao Euler lại quan tâm đến một vấn đề không liên quan đến lĩnh vực toán học như vậy? Tại sao một nhà toán học vĩ đại như vậy lại dành nhiều thời gian cho một bài toán tầm thường như bài toán cây cầu Konigsberg? Euler rõ ràng là một người bận rộn, đã xuất bản hơn 500 cuốn sách và bài báo trong suốt cuộc đời của mình. Riêng năm 1775, trung bình mỗi tuần ông viết một bài báo toán học, và trong suốt cuộc đời mình, ông viết về nhiều chủ đề khác nhau ngoài toán học bao gồm cơ học, quang học, thiên văn học, hàng hải và thủy động lực học. Không có gì đáng ngạc nhiên khi Euler cảm thấy vấn đề này thật tầm thường, ông viết trong một bức thư năm 1736 gửi cho Carl Leonhard Gottlieb Ehler, thị trưởng của Danzig, người đã nhờ ông đưa ra lời giải cho bài toán:
“…Vì vậy, thưa ngài, ngài thấy đấy, bài toán này ít liên quan đến toán học như thế nào, và tôi không hiểu tại sao ngài lại mong đợi một nhà toán học tìm ra nó chứ không phải bất kỳ ai khác, vì lời giải chỉ dựa trên lý trí và khám phá ra nó. Không phụ thuộc vào bất kỳ nguyên tắc toán học nào. Vì điều này, tôi không biết tại sao ngay cả những câu hỏi ít liên quan đến toán học cũng được các nhà toán học giải nhanh hơn những người khác.”
Mặc dù Euler thấy vấn đề tầm thường nhưng ông vẫn bị hấp dẫn bởi nó. Trong một bức thư viết cùng năm cho Giovanni Marinoni, một nhà toán học và kỹ sư người Ý, Euler nói:
“Câu hỏi này thật tầm thường, nhưng đối với tôi, dường như nó đáng được chú ý bởi cả hình học, đại số, thậm chí cả nghệ thuật đếm cũng không đủ để giải quyết nó.”
Euler tin rằng vấn đề này có liên quan đến một chủ đề mà Gottfried Wilhelm Leibniz đã từng thảo luận và mong muốn được làm việc cùng, chủ đề mà Leibniz gọi là geometria situs, hay hình học vị trí. Cái gọi là hình học vị trí này là cái ngày nay ta gọi là lý thuyết đồ thị.
Vào ngày 26 tháng 8 năm 1735, Euler công bố một bài báo chứa lời giải cho bài toán cây cầu Konigsberg. Ông giải quyết vấn đề này và một giải pháp chung cho bất kỳ số lượng đảo và bất kỳ số lượng cây cầu nào. Bài báo này, có tên là ‘Solutio problematis ad geometriam situs pertinentis’, sau đó được xuất bản vào năm 1741. Bài viết của Euler được chia thành 21 đoạn được đánh số, và trong phần tiếp theo, một phiên bản đơn giản hóa vài đoạn của Euler sẽ được trình bày.
Trong hai đoạn đầu, ông giới thiệu bài toán cầu Konigsberg. Trong Đoạn 1, Euler nói rằng ông tin rằng vấn đề này liên quan đến hình học, nhưng không phải là hình học được những người đương thời của ông biết rõ, liên quan đến các phép đo và tính toán, mà thay vào đó là một loại Hình học mới, mà Leibniz gọi là hình học vị trí. Sau đó, trong Đoạn 2, Euler giải thích cho khán giả của mình cách thức hoạt động của bài toán Konigsberg. Euler đã cung cấp một bản phác thảo của vấn đề (xem hình dưới) và gọi bảy cây cầu là 
Sau khi nêu câu hỏi mà mình đang cố gắng giải quyết, Euler bắt đầu dùng các phương pháp khác nhau để tìm lời giải. Trong Đoạn 3, Euler nói với người đọc rằng để giải quyết vấn đề cụ thể này, ông có thể viết ra tất cả các đường đi có thể, nhưng kỹ thuật này sẽ mất rất nhiều thời gian và sẽ không hoạt động đối với các cấu trúc lớn hơn với nhiều cầu và đảo hơn. Vì vậy, Euler quyết định tìm một phương pháp khác để giải quyết vấn đề này.
Trong Đoạn 4, ông bắt đầu đơn giản hóa vấn đề bằng cách phát minh ra một hệ thống thuận tiện để biểu diễn việc băng qua một cây cầu. Euler quyết định rằng thay vì sử dụng các chữ cái viết thường để biểu thị việc đi qua một cây cầu, ông sẽ viết các chữ cái viết hoa biểu thị các vùng đất. Chẳng hạn, tham khảo hình dưới của ông, 
Trong Đoạn 6, Euler tiếp tục giải thích chi tiết về phương pháp của mình. Ông nói với độc giả rằng nếu có nhiều hơn một cây cầu có thể đi qua khi đi từ vùng đất này sang vùng đất khác, thì cây cầu nào được sử dụng không quan trọng. Ví dụ, mặc dù có hai cây cầu, 
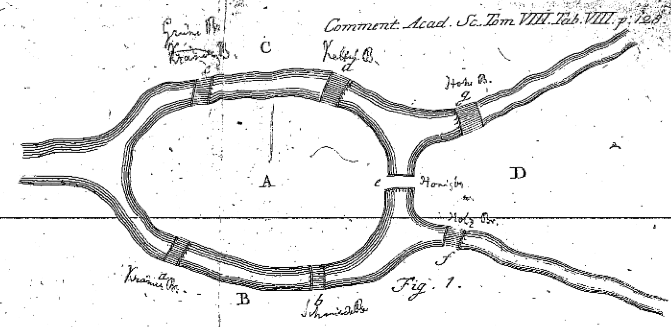
Trong Đoạn 7, Euler cho người đọc biết rằng hoặc anh ta cần tìm một dãy tám chữ cái thỏa mãn bài toán, hoặc anh ta chứng minh rằng không tồn tại dãy nào như vậy. Trước khi làm điều này cho bài toán cầu Konigsberg, ông quyết định tìm một quy tắc để khám phá liệu có tồn tại một đường đi cho một bài toán tổng quát hơn hay không. Ông làm điều này trong Đoạn 8 bằng cách xem xét ví dụ đơn giản hơn nhiều về các vùng đất và cây cầu. Euler vẽ Hình 2, và ông bắt đầu xét các tình huống mà vùng 
Sử dụng phát hiện này, Euler giải bài toán cây cầu Konigsberg trong Đoạn 9. Trong trường hợp này, vì có năm cây cầu dẫn đến 
Khi đọc bài báo của Euler, người ta thấy một công trình toán học tương đối đơn giản và dễ hiểu; tuy nhiên, không phải là những chứng minh mà là các bước trung gian làm cho vấn đề này trở nên nổi tiếng. Sự đổi mới vĩ đại của Euler là xem xét bài toán cây cầu Konigsberg một cách trừu tượng, bằng cách sử dụng các đường kẻ và chữ cái để biểu diễn tình huống tổng quát hơn các vùng đất và cây cầu. Ông đã sử dụng các chữ in hoa để biểu thị các vùng đất và các chữ cái viết thường để biểu thị các cây cầu. Đây là một cách nghĩ hoàn toàn mới vào thời điểm đó, và trong bài báo của mình, Euler đã vô tình khơi dậy một ngành toán học mới gọi là lý thuyết đồ thị, trong đó đồ thị chỉ đơn giản là một tập hợp các đỉnh và các cạnh. Ngày nay, vì bài toán này, một đường đi trong đồ thị chứa mỗi cạnh của đồ thị đúng một lần, được gọi là đường đi Euler. Từ khi Euler giải bài toán này cho đến nay, lý thuyết đồ thị đã trở thành một ngành toán học quan trọng.
T's Lab 
3 thoughts on “Seven bridges of Konigsberg”