Các bạn học sinh chắc rất quen thuộc với cuốn từ điển ANH – VIỆT đúng không? Hôm nay tôi sẽ giới thiệu vài trang trong cuốn từ điển SỐ NGUYÊN – ĐA THỨC. Để theo bài cho dễ dàng các bạn nên đọc lướt qua các bài sau:
[1] https://nttuan.org/2023/06/30/poly01/
[2] https://nttuan.org/2023/07/14/divisibility/
[3] https://nttuan.org/2023/08/04/prime/
Mục đích của bài này là giới thiệu một số kết quả về đa thức tương tự với các kết quả trong số học sơ cấp (xem [2] và [3]), chẳng hạn như thuật toán chia, thuật toán Euclid, và định lí cơ bản của số học. Bởi vì chúng thực sự rất tương tự nên một số chứng minh sẽ bị bỏ qua, hoặc viết vắn tắt. Các em học sinh nên viết lại cẩn thận tất cả các chứng minh để hiểu thêm về đa thức.
Trong bài  là
là  hay
hay 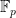 .
.
Định lí 1 (Thuật toán chia). Cho  và
và  là các phần tử của
là các phần tử của ![K[x]](https://s0.wp.com/latex.php?latex=K%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) với
với  . Khi đó tồn tại duy nhất cặp phần tử
. Khi đó tồn tại duy nhất cặp phần tử  của
của ![K[x]](https://s0.wp.com/latex.php?latex=K%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) thỏa mãn
thỏa mãn  và
và  hoặc
hoặc  .
.
Chứng minh. Khẳng định là đúng một cách hiển nhiên nếu  hoặc bậc của
hoặc bậc của  bé hơn bậc của
bé hơn bậc của 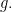 Bây giờ ta xét trường hợp còn lại và chứng minh nó bằng quy nạp theo bậc của
Bây giờ ta xét trường hợp còn lại và chứng minh nó bằng quy nạp theo bậc của  .
.
Nếu bậc của  bằng
bằng 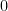 thì bậc của
thì bậc của  bằng
bằng 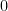 và khẳng định là đúng. Giả sử khẳng định đúng với mọi đa thức
và khẳng định là đúng. Giả sử khẳng định đúng với mọi đa thức  có bậc bé hơn
có bậc bé hơn  . Xét một đa thức
. Xét một đa thức  có bậc
có bậc  và một đa thức
và một đa thức  khác không có bậc
khác không có bậc  . Viết
. Viết  và
và 
Xét đa thức  Ta có
Ta có  có bậc bé hơn
có bậc bé hơn  hoặc
hoặc  nên theo giả thiết quy nạp, ta có thể viết
nên theo giả thiết quy nạp, ta có thể viết  trong đó bậc của
trong đó bậc của  bé hơn
bé hơn  hoặc
hoặc  . Từ đây ta có
. Từ đây ta có  Bây giờ ta đi chứng minh phần còn lại, thương và dư là duy nhất. Giả sử
Bây giờ ta đi chứng minh phần còn lại, thương và dư là duy nhất. Giả sử  và
và  Khi đó
Khi đó  Nếu
Nếu  thì bậc của
thì bậc của  không bé hơn bậc của
không bé hơn bậc của  , trong khi bậc của
, trong khi bậc của  bé hơn bậc của
bé hơn bậc của  , vô lý. Vậy
, vô lý. Vậy  , và đương nhiên
, và đương nhiên  .
. 
Định nghĩa 1. Cho hai đa thức không đồng thời bằng không  và
và  với hệ số trong
với hệ số trong  . Một đa thức monic
. Một đa thức monic  với hệ số trong
với hệ số trong  được gọi là ước chung lớn nhất của
được gọi là ước chung lớn nhất của  và
và  nếu
nếu
(1)  là một ước của
là một ước của  và
và  , và
, và
(2) mỗi ước của  và
và  cũng là một ước của
cũng là một ước của  .
.
Ước chung lớn nhất của  và
và  được ký hiệu bởi
được ký hiệu bởi  . Nếu
. Nếu  thì ta nói
thì ta nói  và
và  nguyên tố cùng nhau.
nguyên tố cùng nhau.
Ước chung lớn nhất nếu có sẽ là duy nhất. Thật vậy, giả sử  và
và  cùng là ước chung lớn nhất của
cùng là ước chung lớn nhất của  và
và  . Khi đó
. Khi đó  và
và  , suy ra
, suy ra  và
và  , do đó
, do đó  Từ đây ta có
Từ đây ta có  , suy ra
, suy ra  và
và  đều có bậc không. Do đó
đều có bậc không. Do đó  bằng
bằng  nhân với một đa thức hằng, nhưng chúng cùng monic nên
nhân với một đa thức hằng, nhưng chúng cùng monic nên  . Định lí sau chứng tỏ ước chung lớn nhất tồn tại.
. Định lí sau chứng tỏ ước chung lớn nhất tồn tại.
Định lí 2. Với các đa thức không đồng thời bằng không ![f, g \in K[x]](https://s0.wp.com/latex.php?latex=f%2C+g+%5Cin+K%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) , ước chung lớn nhất tồn tại và có thể biểu diễn dưới dạng
, ước chung lớn nhất tồn tại và có thể biểu diễn dưới dạng  với
với ![a,b \in K[x]](https://s0.wp.com/latex.php?latex=a%2Cb+%5Cin+K%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) .
.
Chứng minh. Xét tập hợp ![I=\{a f+b g \mid a, b \in K[x]\}.](https://s0.wp.com/latex.php?latex=I%3D%5C%7Ba+f%2Bb+g+%5Cmid+a%2C+b+%5Cin+K%5Bx%5D%5C%7D.&bg=ffffff&fg=000000&s=0&c=20201002) Tập hợp
Tập hợp 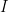 chứa ít nhất một đa thức khác không nên tồn tại đa thức monic
chứa ít nhất một đa thức khác không nên tồn tại đa thức monic  thuộc
thuộc 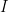 mà có bậc nhỏ nhất. Dễ chứng minh được
mà có bậc nhỏ nhất. Dễ chứng minh được  .
. 
Thuật toán Euclid. Cho ![f, g \in K[x]](https://s0.wp.com/latex.php?latex=f%2C+g+%5Cin+K%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) là hai đa thức khác không. Dùng thuật toán chia ta có
là hai đa thức khác không. Dùng thuật toán chia ta có  trong đó
trong đó  hoặc
hoặc  . Nếu
. Nếu  thì
thì  chia hết
chia hết  , do đó
, do đó  với
với  . Nếu không, ta có tập các ước chung của
. Nếu không, ta có tập các ước chung của  và
và  bằng tập các ước chung của
bằng tập các ước chung của  và
và  , do đó
, do đó  . Quy trình này làm giảm bậc của đa thức nên nó phải kết thức sau hữu hạn bước, lúc đó ta tìm được
. Quy trình này làm giảm bậc của đa thức nên nó phải kết thức sau hữu hạn bước, lúc đó ta tìm được  . Tương tự như với số nguyên, dùng thuật toán này ta có thể tìm được các đa thức
. Tương tự như với số nguyên, dùng thuật toán này ta có thể tìm được các đa thức  và
và  sao cho
sao cho 
Định lí 3. Cho ![f, g,h \in K[x]](https://s0.wp.com/latex.php?latex=f%2C+g%2Ch+%5Cin+K%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) với
với  và
và  . Khi đó
. Khi đó  .
.
Chứng minh. Bạn đọc tự chứng minh xem như bài tập. 
Định nghĩa 2. Một đa thức khác hằng với hệ số trong  được gọi là bất khả quy trên
được gọi là bất khả quy trên  nếu nó không thể phân tích trong
nếu nó không thể phân tích trong ![K[x]](https://s0.wp.com/latex.php?latex=K%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) thành tích của hai đa thức có bậc nhỏ hơn. Nó được gọi là khả quy trên
thành tích của hai đa thức có bậc nhỏ hơn. Nó được gọi là khả quy trên  nếu có phân tích như vậy.
nếu có phân tích như vậy.
Ví dụ. Đa thức  bất khả quy trên
bất khả quy trên 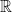 nhưng khả quy trên
nhưng khả quy trên 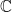 .
.
Tất cả những đa thức bậc 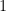 là bất khả quy trên
là bất khả quy trên  . Mỗi đa thức có bậc lớn hơn
. Mỗi đa thức có bậc lớn hơn 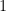 có nghiệm trong
có nghiệm trong  sẽ khả quy trên
sẽ khả quy trên  . Ngược lại không đúng, một đa thức khả quy vẫn có thể không có nghiệm trong
. Ngược lại không đúng, một đa thức khả quy vẫn có thể không có nghiệm trong  . Tuy nhiên, với các đa thức bậc
. Tuy nhiên, với các đa thức bậc  hay
hay  ta có kết quả sau:
ta có kết quả sau:
Định lí 4. Một đa thức có bậc  hay
hay  bất khả quy trên
bất khả quy trên  khi và chỉ khi nó không có nghiệm trong
khi và chỉ khi nó không có nghiệm trong  .
.
Tương tự như với số nguyên ta có các định lí sau. Bạn đọc tự chứng minh chúng xem như bài tập.
Định lí 5. Đa thức khác hằng ![p \in K[x]](https://s0.wp.com/latex.php?latex=p+%5Cin+K%5Bx%5D&bg=ffffff&fg=000000&s=0&c=20201002) bất khả quy trên
bất khả quy trên  khi và chỉ khi với mỗi
khi và chỉ khi với mỗi ![f,g \in K[x],](https://s0.wp.com/latex.php?latex=f%2Cg+%5Cin+K%5Bx%5D%2C&bg=ffffff&fg=000000&s=0&c=20201002)
 kéo theo
kéo theo  hoặc
hoặc  .
.
Định lí 6. Mỗi đa thức khác hằng với hệ số trong  có thể viết như là một phần tử của
có thể viết như là một phần tử của  nhân với tích của các đa thức monic bất khả quy trên
nhân với tích của các đa thức monic bất khả quy trên  . Nếu không kể đến thứ tự của các nhân tử thì biểu diễn này là duy nhất.
. Nếu không kể đến thứ tự của các nhân tử thì biểu diễn này là duy nhất.
Continue reading “Z – K[x]” →
lớn hơn
có đúng hai ước dương là
và
. Một số nguyên lớn hơn
được gọi là hợp số nếu nó không phải là số nguyên tố. Các số
và
là các số nguyên tố. Các số
và
là các hợp số.
có thể biểu diễn như là tích của các số nguyên tố.
là một số nguyên lớn hơn
. Nếu
là số nguyên tố thì nó là tích với một thừa số nguyên tố. Nếu không thì
, trong đó
và
là các số nguyên lớn hơn
và bé hơn
. Nếu
là một số nguyên tố, ta không làm gì; nếu không thì viết
thành tích của hai số nguyên lớn hơn
và bé hơn
; thao tác tương tự với
. Tiếp tục thao tác như thế trên các thừa số mới. Quá trình này phải dừng vì không có dãy giảm nghiêm ngặt gồm vô hạn số nguyên dương, khi đó ta có một cách biểu diễn
như là tích của các số nguyên tố.
lớn hơn
có thể viết được dưới dạng
là các số nguyên tố phân biệt và
là các số nguyên dương. Biểu diễn này được gọi là phân tích chính tắc của
thành các lũy thừa nguyên tố. Ta sẽ chứng minh rằng biểu diễn này là duy nhất theo nghĩa: đối với mỗi
, bất kỳ biểu diễn nào khác chỉ là sự sắp xếp lại các thừa số.