Nguyên lý thứ nhất (Quy tắc cộng). Giả sử có 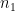 cách thực hiện việc
cách thực hiện việc 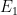 ,
, 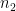 cách thực hiện việc
cách thực hiện việc 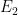 ,…,
,…,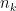 cách thực hiện việc
cách thực hiện việc  . Nếu
. Nếu  việc này không thể làm đồng thời thì sẽ có
việc này không thể làm đồng thời thì sẽ có  cách thực hiện một trong các việc
cách thực hiện một trong các việc  .
.
Ví dụ 1. Người ta có thể đi từ Hải Phòng đến Đà Nẵng bằng một trong ba phương tiện: tàu hoả, tàu thuỷ và máy bay. Nếu có hai cách đi bằng tàu hoả, ba cách đi bằng tàu thuỷ, và 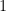 cách đi bằng máy bay thì sẽ có
cách đi bằng máy bay thì sẽ có  cách đi từ Hải Phòng đến Đà Nẵng.
cách đi từ Hải Phòng đến Đà Nẵng. 
Ví dụ 2. Tìm số các cặp có thứ tự  các số nguyên thoả mãn
các số nguyên thoả mãn  .
.
Lời giải. Mỗi  ta đặt
ta đặt  , khi đó tập cần tính số phần tử sẽ là hợp rời rạc của các
, khi đó tập cần tính số phần tử sẽ là hợp rời rạc của các 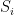 . Ta tính số phần tử của các
. Ta tính số phần tử của các 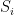 bằng phương pháp liệt kê và cuối cùng được đáp số của bài toán là
bằng phương pháp liệt kê và cuối cùng được đáp số của bài toán là 

Nguyên lý thứ hai (Quy tắc nhân). Giả sử rằng việc 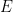 có thể được làm bằng cách thực hiện liên tiếp các việc
có thể được làm bằng cách thực hiện liên tiếp các việc  ; và có
; và có 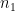 cách thực hiện việc
cách thực hiện việc 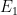 ,
, 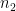 cách thực hiện việc
cách thực hiện việc 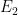 ,…,
,…,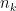 cách thực hiện việc
cách thực hiện việc  . Khi đó số cách làm việc
. Khi đó số cách làm việc 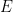 là
là  .
.
Ví dụ 3. Đề đi từ thành phố  đến thành phố
đến thành phố 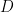 người ta phải đi lần lượt qua hai thành phố
người ta phải đi lần lượt qua hai thành phố 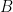 và
và 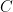 . Nếu có hai cách đi từ
. Nếu có hai cách đi từ  đến $B$, ba cách đi từ
đến $B$, ba cách đi từ 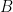 đến
đến 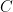 và một cách đi từ
và một cách đi từ 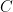 đến
đến 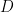 thì sẽ có
thì sẽ có  cách đi từ
cách đi từ  đến
đến 

Ví dụ 4. Cho  và
và  là các số nguyên dương. Một dãy
là các số nguyên dương. Một dãy  phân độ dài
phân độ dài  là một dãy
là một dãy  với
với  . Hỏi có bao nhiêu dãy này?
. Hỏi có bao nhiêu dãy này?
Lời giải. Đặt  . Để hình thành một dãy
. Để hình thành một dãy  phân, đầu tiên chúng ta cần chọn
phân, đầu tiên chúng ta cần chọn 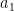 từ
từ 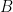 , sau đó chọn
, sau đó chọn 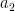 từ
từ 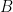 , và cứ như thế cho đến cuối cùng cần chọn
, và cứ như thế cho đến cuối cùng cần chọn 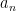 từ
từ 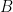 . Bởi vì có
. Bởi vì có  cách để làm mỗi bước nên theo quy tắc nhân, số các dãy như vậy bằng
cách để làm mỗi bước nên theo quy tắc nhân, số các dãy như vậy bằng 

Ví dụ 5. Tìm số các ước dương của  .
.
Lời giải. Ta có  nên một số nguyên dương
nên một số nguyên dương  là một ước dương của
là một ước dương của  khi và chỉ khi nó có dạng
khi và chỉ khi nó có dạng  với
với 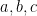 là các số nguyên thoả mãn
là các số nguyên thoả mãn  . Như vậy số các ước dương của
. Như vậy số các ước dương của  bằng số các bộ ba
bằng số các bộ ba 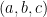 thoả mãn
thoả mãn  , theo quy tắc nhân, số ước dương của
, theo quy tắc nhân, số ước dương của  bằng
bằng 

Tổng quát hơn ta có: Nếu số nguyên dương  có phân tích tiêu chuẩn
có phân tích tiêu chuẩn  thì số các ước dương của
thì số các ước dương của  bằng
bằng  .
.
Ví dụ 6. Cho  và
và
 Tính
Tính  .
.
Lời giải. Với mỗi  ta đặt
ta đặt  . Khi đó
. Khi đó  là hợp rời rạc của các
là hợp rời rạc của các 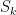 , mà theo quy tắc nhân ta có
, mà theo quy tắc nhân ta có  nên suy ra
nên suy ra  .
.
Để ý đến lời giải ví dụ thứ hai và thứ sáu, ta thấy chúng có một điểm chung là chia bài toán đã cho thành các bài toán con đơn giản hơn và giải chúng. Đây là cách cơ bản nhất để giải các bài toán đếm, có thể sẽ có cách khác ngắn gọn hơn, nhưng việc chia một bài toán thành các bài toán con mà chúng ta đã biết cách giải sẽ giúp ta ít gặp phải các sai lầm hơn.
Ví dụ 7. Có bao nhiêu số tự nhiên có ba chữ số được lấy từ tập  nếu
nếu
(a) Các chữ số không cần phải khác nhau?
(b) Các chữ số phải khác nhau?
(c) Các chữ số phải khác nhau và chứa số  ?
?
(d) Các chữ số không cần phải khác nhau và chứa số  ?
?
Lời giải.
(a) 
(b)  .
.
(c) Đầu tiên ta chọn vị trí cho số  , sau đó chọn hai số còn lại lần lượt. Đáp số là
, sau đó chọn hai số còn lại lần lượt. Đáp số là  .
.
(d) Nếu tiếp tục làm như trên ta sẽ được kết quả là  , đây là một kết quả không chính xác! Vì làm như vậy những số như
, đây là một kết quả không chính xác! Vì làm như vậy những số như  sẽ được đếm hai lần. Vấn đề ở chỗ ta đã dùng sai quy tắc nhân, mỗi hai tổ hợp khác nhau cách thực hiện các công việc
sẽ được đếm hai lần. Vấn đề ở chỗ ta đã dùng sai quy tắc nhân, mỗi hai tổ hợp khác nhau cách thực hiện các công việc  phải cho hai kết quả khác nhau thì ta mới áp dụng được quy tắc nhân. Bài này ta lại phải chia thành các bài toán con và giải chúng lần lượt.
phải cho hai kết quả khác nhau thì ta mới áp dụng được quy tắc nhân. Bài này ta lại phải chia thành các bài toán con và giải chúng lần lượt.
Ta chia trường hợp theo vị trí của số  nằm bên trái nhất. Nếu số
nằm bên trái nhất. Nếu số  này nằm ở vị trí hàng trăm thì số có ba chữ số phải có dạng
này nằm ở vị trí hàng trăm thì số có ba chữ số phải có dạng  , nếu nó nằm ở vị trí hàng chục thì số có ba chữ số phải có dạng
, nếu nó nằm ở vị trí hàng chục thì số có ba chữ số phải có dạng  với
với  , và cuối cùng, nếu số
, và cuối cùng, nếu số  này nằm ở vị trí hàng đơn vị thì số ba chữ số phải có dạng
này nằm ở vị trí hàng đơn vị thì số ba chữ số phải có dạng  với
với  . Giải các bài toán con ta được đáp số của bài toán là
. Giải các bài toán con ta được đáp số của bài toán là 

Continue reading “Basic counting principles” →
là một số nguyên dương,
là một số nguyên thoả mãn
và
là một tập hợp có
phần tử. Một
hoán vị của
(hay một chỉnh hợp chập
của
) là một cách xếp
phần tử nào đó của
thành một hàng. Một
hoán vị của
sẽ được gọi là một hoán vị của
. Khi đó các
hoán vị của
là (có tất cả
):
là một số nguyên dương,
là một số nguyên thoả mãn
và
là một tập hợp có
phần tử. Khi đó số
hoán vị của
bằng
. Nói riêng, số hoán vị của
bằng
.
hoán vị của
sẽ được hình thành sau
bước: Đầu tiên, chọn một phần tử từ
và đặt nó vào vị trí thứ nhất; sau đó ta chọn trong các phần tử còn lại của
một phần và đặt nó vào vị trí thứ hai;…; và cuối cùng ta chọn một phần tử từ
phần tử còn lại của
và đặt nó vào vị trí thứ
. Vì có
cách làm bước thứ nhất,
cách làm bước thứ hai;…; và
cách làm bước thứ
nên theo quy tắc nhân, ta có
là tập tất cả
chữ cái tiếng Anh. Tìm số các từ gồm
chữ trong
sao cho chữ đầu tiên, chữ cuối cùng là các nguyên âm phân biệt và ba chữ còn lại là các phụ âm phân biệt.
nguyên âm trong
đó là
và
chữ cái còn lại là các phụ âm. Một từ thỏa mãn yêu cầu của đầu bài sẽ được hình thành sau hai bước: Đầu tiên, chọn một
hoán vị của
và đặt nguyên âm thứ nhất vào vị trí
, nguyên âm thứ hai vào vị trí
, sau đó chọn một
hoán vị của
và đặt phụ âm thứ nhất, hai, ba của hoán vị vào vị trí
tương ứng.
cách để làm bước thứ nhất và
cách để làm bước thứ hai nên theo quy tắc nhân ta có số các từ thoả mãn là
