
Olympic Toán học Quốc tế (IMO) 2025 là kỳ thi toán học danh giá nhất dành cho học sinh trung học, được tổ chức tại Sunshine Coast, Queensland, Australia từ ngày 10 đến 20 tháng 7 năm 2025. Đây là lần thứ 66 của cuộc thi, quy tụ các tài năng toán học trẻ từ hơn 100 quốc gia, tranh tài qua 6 bài toán khó trong các lĩnh vực như đại số, hình học, số học và tổ hợp. Việt Nam, với truyền thống thành tích ấn tượng tại IMO từ năm 1974, tiếp tục cử đội tuyển gồm 6 học sinh xuất sắc tham dự kỳ thi năm nay. Đội tuyển được lựa chọn qua Kỳ thi học sinh giỏi quốc gia và Kỳ thi chọn đội tuyển Olympic quốc tế, thể hiện sự chuẩn bị kỹ lưỡng của Bộ Giáo dục và Đào tạo.
Theo thông tin chính thức, danh sách đội tuyển Việt Nam tham dự IMO 2025 bao gồm:
- Nguyễn Đình Tùng (lớp 11, Trường THPT chuyên Khoa học Tự nhiên, Đại học Quốc gia Hà Nội).
- Trần Minh Hoàng (lớp 12, Trường THPT chuyên Hà Tĩnh).
- Võ Trọng Khải (lớp 12, Trường THPT chuyên Phan Bội Châu, Nghệ An).
- Trương Thanh Xuân (lớp 11, Trường THPT chuyên Bắc Ninh) – nữ sinh duy nhất sau 5 năm.
- Nguyễn Đăng Dũng (lớp 12, Trường THPT chuyên Khoa học Tự nhiên, Đại học Quốc gia Hà Nội).
- Lê Phan Đức Mân (lớp 12, Trường THPT chuyên Lê Hồng Phong, TP. Hồ Chí Minh).
Đội tuyển được dẫn dắt bởi trưởng đoàn TS. Nguyễn Chu Gia Vượng, cựu thí sinh IMO 1993 (HCV) và 1994 (HCB), và phó đoàn TS. Lê Bá Khánh Trình, người từng giành giải đặc biệt tại IMO 1979. Cả hai đều là những chuyên gia dày dạn kinh nghiệm trong bồi dưỡng học sinh giỏi.
Dưới đây là đề thi và kết quả.
Đề thi:
Những bài toán này được thiết kế để thử thách các học sinh trung học hàng đầu thế giới, bao gồm các lĩnh vực cốt lõi của toán học trung học: đại số, hình học, lý thuyết số và tổ hợp.
Các bài toán IMO thường được thiết kế theo hướng tăng dần độ khó theo từng ngày, với Bài toán 1 (P1) và Bài toán 4 (P4) thường dễ tiếp cận nhất, Bài toán 2 (P2) và 5 (P5) có độ khó trung bình, và Bài toán 3 (P3) và 6 (P6) là khó nhất. Đối với IMO 2025, mô hình này dường như vẫn được duy trì dựa trên phản hồi từ AoPS, một diễn đàn nổi tiếng về toán Olympiad.
Kết quả của đội Việt Nam: 2 HCV, 3 HCB, và 1 HCĐ. Cụ thể: Khải và Hoàng đạt HCV; Dũng, Tùng và Mân đạt HCB; Xuân đạt HCĐ. Đội đứng thứ 9 về tổng điểm.

Các thí sinh có điểm cao nhất:
Em Khải góp mặt ở vị trí 8. 🙂 Có lẽ vì bài 2 và bài 3 quá dễ mà điểm để đạt HCV rất cao, 35 điểm!

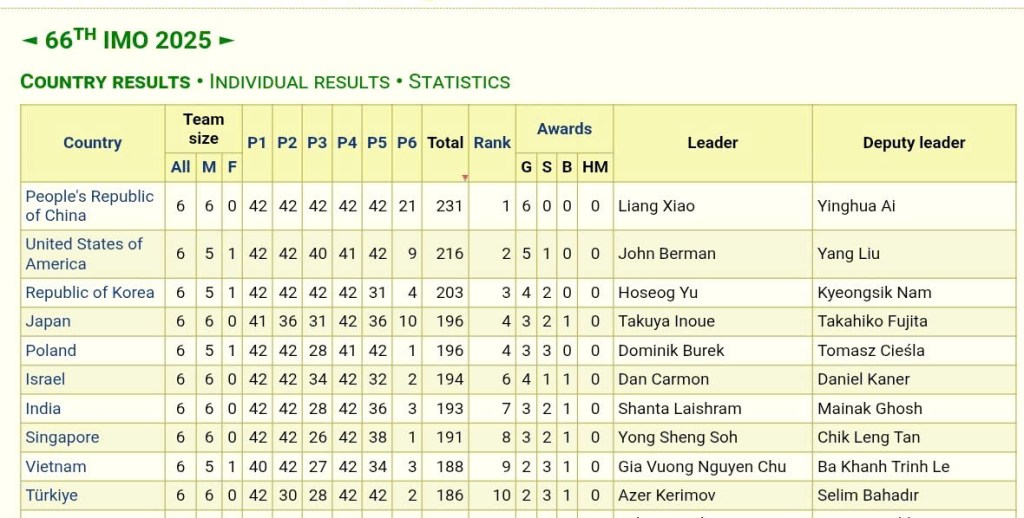
10 đội có tổng điểm cao nhất:
Đội Việt Nam đứng thứ 9. 🙂
Kết thúc cuộc thi, BTC cũng vừa công bố IMO2024SL.
