IMO Shortlist 2024: Geometry

Trong bài này tôi sẽ giới thiệu các bài toán hình học trong cuốn IMO Shortlist 2024, các bài toán từ IMO SL năm trước các bạn có thể tìm ở https://nttuan.org/category/contests/imo-shortlist/

G1. https://artofproblemsolving.com/community/c6h3610481p35341119

Cho $ABCD$ là tứ giác nội tiếp sao cho $AC<BD<AD$ và $\angle DBA<90^\circ$ . Điểm $E$ nằm trên đường thẳng đi qua $D$ song song với $AB$ sao cho $E$ và $C$ nằm khác phía đối với $AD$ và $AC=DE$ . Điểm $F$ nằm trên đường thẳng đi qua $A$ song song với $CD$ sao cho $F$ và $C$ nằm khác phía đối với $AD$ và $BD=AF$ . Chứng minh rằng các đường trung trực của $BC$ và $EF$ cắt nhau trên đường tròn ngoại tiếp của $ABCD$ .

G2. https://artofproblemsolving.com/community/c6h3359767p31218657

Cho $ABC$ là một tam giác với $AB < AC < BC$ . Gọi tâm đường tròn nội tiếp và đường tròn nội tiếp của tam giác $ABC$ lần lượt là $I$ và $\omega$ . Gọi $X$ là điểm trên đường thẳng $BC$ , khác $C$ , sao cho đường thẳng qua $X$ song song với $AC$ tiếp xúc với $\omega$ . Tương tự, gọi $Y$ là điểm trên đường thẳng $BC$ , khác $B$ , sao cho đường thẳng qua $Y$ song song với $AB$ tiếp xúc với $\omega$ . Đường thẳng $AI$ cắt lại đường tròn ngoại tiếp tam giác $ABC$ tại $P$ . Gọi $K$ và $L$ lần lượt là trung điểm của $AC$ và $AB$ . Chứng minh rằng $\angle KIL + \angle YPX = 180^{\circ}$ . (IMO2024/4)

G3. https://artofproblemsolving.com/community/c6h3610478p35341061

Cho $ABCDE$ là một ngũ giác lồi và $M$ là trung điểm của $AB$ . Giả sử $AB$ tiếp tuyến với đường tròn ngoại tiếp tam giác $CME$ tại $M$ và $D$ nằm trên các đường tròn ngoại tiếp của $AME$ và $BMC$ . Các đường thẳng $AD$ và $ME$ cắt nhau tại $K$ , và các đường thẳng $BD$ và $MC$ cắt nhau tại $L$ . Các điểm $P$ và $Q$ nằm trên đường thẳng $EC$ sao cho $\angle PDC = \angle EDQ = \angle ADB$ . Chứng minh rằng các đường thẳng $KP, LQ,$ và $MD$ đồng quy.

G4. https://artofproblemsolving.com/community/c6h3610440p35340910

Cho $ABCD$ là tứ giác có $AB$ song song với $CD$ và $AB<CD$ . Hai đường thẳng $AD$ và $BC$ cắt nhau tại $P$ . Điểm $X$ khác $C$ nằm trên đường tròn ngoại tiếp tam giác $ABC$ sao cho $PC=PX$ . Điểm $Y$ khác $D$ nằm trên đường tròn ngoại tiếp tam giác $ABD$ sao cho $PD=PY$ . Hai đường thẳng $AX$ và $BY$ cắt nhau tại $Q$ . Chứng minh rằng $PQ$ song song với $AB$ .

G5. https://artofproblemsolving.com/community/c6h3610468p35340974

Cho tam giác $ABC$ có tâm nội tiếp $I$ , và $\Omega$ là đường tròn ngoại tiếp tam giác $BIC$ . Cho $K$ là một điểm nằm trong đoạn thẳng $BC$ sao cho $\angle BAK < \angle KAC$ . Đường phân giác của $\angle BKA$ cắt $\Omega$ tại các điểm $W$ và $X$ sao cho $A$ và $W$ nằm cùng một phía đối với $BC$ , và đường phân giác của $\angle CKA$ cắt $\Omega$ tại các điểm $Y$ và $Z$ sao cho $A$ và $Y$ nằm cùng một phía đối với $BC$ . Chứng minh rằng $\angle WAY = \angle ZAX$ .

G6. https://artofproblemsolving.com/community/c6h3610439p35340907

Cho $ABC$ là tam giác nhọn với $AB < AC$ , và $\Gamma$ là đường tròn ngoại tiếp $ABC$ . Các điểm $X$ và $Y$ nằm trên $\Gamma$ sao cho $XY$ và $BC$ cắt nhau trên đường phân giác ngoài của $\angle BAC$ . Giả sử các tiếp tuyến của $\Gamma$ tại $X$ và $Y$ cắt nhau tại điểm $T$ nằm cùng phía với $A$ đối với $BC$ , và $TX$ và $TY$ cắt $BC$ tại $U$ và $V$ , tương ứng. Gọi $J$ là tâm của đường tròn bàng tiếp đối diện đỉnh $T$ của tam giác $TUV$ . Chứng minh rằng $AJ$ là phân giác của $\angle BAC$ .

G7. https://artofproblemsolving.com/community/c6h3610452p35340925

Cho $ABC$ là tam giác có tâm nội tiếp $I$ sao cho $AB<AC<BC$ . Giao điểm thứ hai của $AI, BI$ , và $CI$ với đường tròn ngoại tiếp tam giác $ABC$ lần lượt là $M_{A}$ , $M_{B}$ , và $M_{C}$ . Các đường thẳng $AI$ và $BC$ cắt nhau tại $D$ và các đường thẳng $BM_{C}$ và $CM_{B}$ cắt nhau tại $X$ . Giả sử đường tròn ngoại tiếp tam giác $XM_{B}M_{C}$ và $XBC$ cắt nhau tại $S\neq X$ . Các đường thẳng $BX$ và $CX$ cắt lại đường tròn ngoại tiếp tam giác $SXM_{A}$ tại $P\neq X$ và $Q\neq X$ , tương ứng. Chứng minh rằng tâm đường tròn ngoại tiếp tam giác $SID$ nằm trên $PQ$ .

G8. https://artofproblemsolving.com/community/c6h3610449p35340922

Cho tam giác $ABC$ có $AB<AC<BC$ , và $D$ là một điểm nằm trong đoạn thẳng $BC$ . Cho $E$ là một điểm trên đường tròn ngoại tiếp tam giác $ABC$ sao cho $A$ và $E$ nằm khác phía đối với $BC$ và $\angle{BAD}=\angle{EAC}$ . Gọi $I,I_B,I_C,J_B$ và $J_C$ lần lượt là tâm nội tiếp của các tam giác $ABC,ABD,ADC,ABE$ và $AEC$ . Chứng minh rằng $I_B,I_C,J_B$ và $J_C$ đồng viên khi và chỉ khi $AI,I_BJ_C$ và $J_BI_C$ đồng quy.

IMO2025/3

Trong bài này tôi sẽ giới thiệu một lời giải của bài 3 trong đề IMO 2025. Đề thi đầy đủ tôi đã đăng ở đây: https://nttuan.org/2025/07/01/imo-2025-problems-and-results/ .

IMO2025/3. Một hàm $f:\mathbb{N}^*\to\mathbb{N}^*$ được gọi là bonza nếu $f(a)\mid b^a-f(b)^{f(a)}$ với mọi số nguyên dương $a$ và $b$ .
Xác định hằng số thực nhỏ nhất $c$ sao cho $f(n)\leqslant cn$ với mọi hàm bonza $f$ và mọi số nguyên dương $n$ .

imo2025p3 Download

IMO Shortlist 2023: Combinatorics

Hình học : https://nttuan.org/2024/11/02/isl2023-geometry/

Đại số: https://nttuan.org/2025/01/23/isl2023-algebra/

Số học: https://nttuan.org/2025/02/13/isl2023-number-theory/

C1. https://artofproblemsolving.com/community/c6h3359749p31218491

Cho $m$ và $n$ là các số nguyên lớn hơn $1$ . Trong mỗi ô vuông đơn vị của lưới $m\times n$ có một đồng xu với mặt trái hướng lên trên. Một phép toán bao gồm các bước sau.

chọn một hình vuông $2\times 2$ trong lưới;
lật các đồng xu ở ô đơn vị trên cùng bên trái và dưới cùng bên phải;
lật đồng xu ở ô vuông đơn vị trên cùng bên phải hoặc dưới cùng bên trái.

Xác định tất cả các cặp $(m,n)$ sao cho mọi đồng xu đều hiện mặt phải sau một số hữu hạn lần thực hiện phép toán.

C2. https://artofproblemsolving.com/community/c6h3359755p31218537

Xác định số nguyên dương $L$ lớn nhất sao cho tồn tại một dãy các số nguyên dương $a_1,\dots,a_L$ có tính chất: mỗi số hạng của dãy không lớn hơn $2^{2023}$ , và không có các số hạng liên tiếp $a_i,a_{i+1},\dots,a_j$ (ở đây $1\le i\le j\le L$ ) với một cách chọn dấu $s_i,s_{i+1},\dots,s_j\in\{1,-1\}$ để

$s_ia_i+s_{i+1}a_{i+1}+\dots+s_ja_j=0.$

C3. https://artofproblemsolving.com/community/c6h3107350p28104367

Cho $n$ là một số nguyên dương. Một tam giác Nhật Bản gồm $1+2+\cdots+n$ hình tròn được xếp thành một hình tam giác đều sao cho với mỗi $i = 1, 2, ..., n$ , hàng thứ $i$ có đúng $i$ hình tròn và trên hàng đó có đúng một hình tròn được tô màu đỏ. Một đường đi ninja trong một tam giác Nhật Bản là một dãy gồm $n$ hình tròn nhận được bằng cách xuất phát từ hàng trên cùng, đi lần lượt từ một hình tròn xuống một trong hai hình tròn ngay dưới nó, và kết thúc tại hàng dưới cùng. Trong hình vẽ là một tam giác Nhật Bản với $n = 6$ và một đường đi ninja có chứa hai hình tròn màu đỏ.

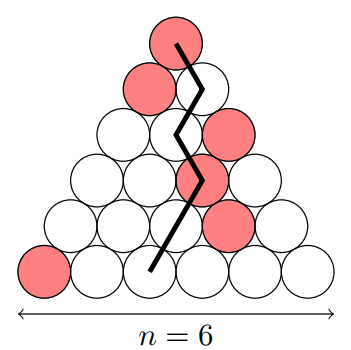
Như một hàm số của $n$ , tìm giá trị lớn nhất của $k$ sao cho trong mỗi tam giác Nhật Bản luôn có một đường đi ninja chứa ít nhất $k$ hình tròn màu đỏ. (IMO2023/5)

C4. https://artofproblemsolving.com/community/c6h3359724p31218375

Cho $n\geqslant 2$ là một số nguyên dương. Paul có một dải hình chữ nhật cỡ $1\times n^2$ gồm $n^2$ hình vuông đơn vị, trong đó hình vuông thứ $i$ được gắn nhãn $i$ với mọi $1\leqslant i\leqslant n^2$ . Anh ta muốn cắt dải giấy thành nhiều mảnh, trong đó mỗi mảnh bao gồm một số ô vuông đơn vị liên tiếp, sau đó dịch chuyển (không xoay hoặc lật) các mảnh để thu được hình vuông $n\times n$ thỏa mãn tính chất sau: nếu hình vuông đơn vị trong hàng $i$ và cột $j$ được gắn nhãn $a_{ij}$ , thì $a_{ij}-(i+j -1)$ chia hết cho $n$ .

Xác định số mảnh nhỏ nhất mà Paul cần tạo để hoàn thành việc này.

C5. https://artofproblemsolving.com/community/c6h3359765p31218619

Elisa có $latex $2023$ rương kho báu, tất cả đều được mở khóa và trống rỗng lúc đầu. Mỗi ngày, Elisa thêm một viên đá quý mới vào một trong những chiếc rương đã mở khóa mà cô ấy chọn, và sau đó, một cô tiên sẽ hành động theo các quy tắc sau:

nếu có nhiều hơn một rương được mở khóa, cô sẽ khóa một trong số chúng, hoặc
nếu chỉ có một rương được mở khóa, cô sẽ mở khóa tất cả các rương.

Cho rằng quá trình này diễn ra mãi mãi, hãy chứng minh rằng tồn tại một hằng số $C$ với tính chất sau: Elisa có thể đảm bảo rằng chênh lệch giữa số viên ngọc trong hai rương bất kỳ không bao giờ vượt quá $latex $C$, bất kể cô tiên hành động như thế nào.

C6. https://artofproblemsolving.com/community/c6h3359747p31218478

Cho $N$ là một số nguyên dương và xét một lưới $N \times N$ các ô vuông. Đường dẫn xuống bên phải là một dãy các ô lưới sao cho mỗi ô là một ô ở bên phải hoặc một ô bên dưới ô trước đó trong chuỗi. Đường dẫn lên bên phải là một chuỗi các ô lưới sao cho mỗi ô là một ô ở bên phải hoặc một ô phía trên ô trước đó trong chuỗi.

Chứng minh rằng không thể phân chia các ô của lưới $N \times N$ thành ít hơn $N$ vùng sao cho mỗi vùng là một đường dẫn xuống bên phải xuống hoặc một đường dẫn lên bên phải.

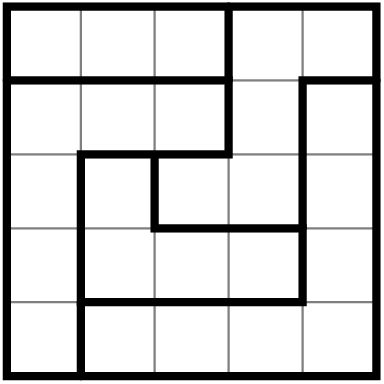
Chẳng hạn, lưới $5 \times 5$ có thể phân chia thành $5$ vùng như hình vẽ.

C7. https://artofproblemsolving.com/community/c6h3359751p31218524

Quần đảo Imomi bao gồm $n\geq 2$ hòn đảo. Giữa mỗi cặp đảo khác nhau có một tuyến phà duy nhất chạy theo cả hai hướng và mỗi tuyến phà được điều hành bởi một trong $k$ công ty. Được biết, nếu bất kỳ công ty nào đóng cửa tất cả các tuyến phà của mình thì một du khách, bất kể bắt đầu từ đâu, sẽ không thể ghé thăm tất cả các hòn đảo đúng một lần (đặc biệt là không quay lại hòn đảo mà du khách bắt đầu). Xác định giá trị lớn nhất có thể có của $k$ theo $n$ .

VMO 2025/1

VMO 2025/1. Xét đa thức $P(x)=x^4-x^3+x$ .
(1) Chứng minh rằng với mỗi số thực dương $a$ , đa thức $P(x)-a$ có duy nhất một nghiệm thực dương.
(2) Xét dãy số $(a_n)_{n\geq 1}$ xác định bởi $a_1=1/3$ và với mỗi số nguyên dương $n$ , $a_{n+1}$ là nghiệm dương của đa thức $P(x)-a_n$ . Chứng minh rằng dãy số này có giới hạn hữu hạn và tìm giới hạn đó.

Lời giải. Xét một số thực dương $a$ và hàm số $f:\mathbb{R}\to\mathbb{R}$ xác định bởi $f(x)=P(x)-a,\quad\forall x\in\mathbb{R}.$ Hàm số $f$ là một hàm số liên tục trên $(0;+\infty)$ và

$\displaystyle \lim_{x\to 0^+} f(x)=-a<0,\quad\lim_{x\to+\infty}f(x)=+\infty,$

từ đây theo định lý giá trị trung gian, phương trình $f(x)=0$ có ít nhất một nghiệm thực dương. Mặt khác, hàm số $f$ đồng biến trên $(0;+\infty)$ vì

$\displaystyle f^{\prime}(x)=4x^3-3x^2+1=(2x-1)^2\left(x+\frac{1}{4}\right)+\frac{3}{4}>0$

với mọi số thực dương $x$ , suy ra phương trình $f(x)=0$ có đúng một nghiệm thực dương. Do đó phương trình $P(x)-a=0$ có đúng một nghiệm thực dương. Nghiệm này là nghiệm đơn của đa thức $P(x)-a$ nên ta có ý thứ nhất.

Bây giờ ta đến với ý thứ hai. Từ giả thiết ta có

$a_n-1=(a_{n+1}-1)(a_{n+1}^3+1),\quad\forall n\geq 1,$

sử dụng phương pháp quy nạp ta chứng minh được tất cả các số hạng của dãy $(a_n)_{n\geq 1}$ đều thuộc khoảng $(0;1)$ . Suy ra

$a_{n+1}-a_n=a_{n+1}^3(1-a_{n+1})>0,\quad\forall n\geq 1,$

do đó $(a_n)_{n\geq 1}$ là một dãy số tăng. Dãy số này cũng bị chặn trên bởi $1$ nên nó có giới hạn hữu hạn. Gọi $L$ là giới hạn của dãy số $(a_n)_{n\geq 1}$ . Vì $(a_n)_{n\geq 1}$ tăng và các số hạng đều thuộc khoảng $(0;1)$ , nên $0<L\leq 1$ .

Từ $P(a_{n+1})=a_n$ với mọi số nguyên dương $n$ , ta có $L^4-L^3+L=L,$ suy ra $\lim a_n=L=1$ . $\Box$

IMO Shortlist 2022: Number theory

N1. Một số nguyên dương được gọi là số Na Uy nếu nó có ba ước dương phân biệt có tổng bằng $2022$ . Xác định số Na Uy nhỏ nhất.

N2. Tìm tất cả các số nguyên dương $n>2$ sao cho

$\displaystyle n! \mid \prod_{ p<q\le n,\quad p,q\in\mathbb{P}} (p+q).$

N3. Cho $a > 1$ là một số nguyên dương và $d > 1$ là một số nguyên dương nguyên tố cùng nhau với $a$ . Đặt $x_1=1$ và với $k\geq 1$ , $x_{k+1} = x_k + d$ nếu không chia hết $x_k$ , $=x_k/a$ nếu $a$ chia hết $x_k$ . Tìm, theo $a$ và $d$ , số nguyên dương $n$ lớn nhất mà tồn tại chỉ số $k$ sao cho $x_k$ chia hết cho $a^n$ .

N4. Tìm tất cả các bộ ba số nguyên dương $(a,b,p)$ sao cho $p$ là số nguyên tố và $a^p=b!+p.$

(IMO2022/5)

N5. Đối với mỗi $i\in [9]$ và $T\in\mathbb{N}^*$ , ký hiệu $d_i(T)$ là số lần chữ số $i$ xuất hiện khi tất cả các bội của $1829$ trong $[T]$ được viết ra theo cơ số $10$ . Chứng minh rằng có vô số $T\in\mathbb{N}^*$ sao cho có đúng hai giá trị phân biệt trong các số $d_1(T)$ , $d_2(T)$ , $\dots$ , $d_9(T)$ .

N6. Cho $Q$ là một tập hợp không nhất thiết hữu hạn các số nguyên tố. Đối với một số nguyên dương $n$ , xét phân tích ra thừa số nguyên tố của nó: gọi $p(n)$ là tổng của tất cả các số mũ và $q(n)$ là tổng của các số mũ tương ứng với các số nguyên tố trong $Q$ . Số nguyên dương $n$ được gọi là đặc biệt nếu $p(n)+p(n+1)$ và $q(n)+q(n+1)$ đều là số nguyên chẵn. Chứng minh rằng tồn tại một hằng số $c>0$ không phụ thuộc $Q$ sao cho với mọi số nguyên dương $N>100$ , số các số nguyên đặc biệt trong $[N]$ ít nhất là $cN$ .

N7. Gọi $k$ là một số nguyên dương và $S$ là một tập hữu hạn các số nguyên tố lẻ. Chứng minh rằng có nhiều nhất một cách (sai khác phép quay và đối xứng) để đặt các phần tử của $S$ xung quanh một đường tròn sao cho tích của hai số cạnh nhau bất kỳ có dạng $x^2+x+k$ với một số nguyên dương $x$ .