Category: Number theory

Continued fractions: The basics


Let x_0, \displaystyle x_1, \displaystyle x_2, \displaystyle \ldots be variables. We define two sequences of polynomials with complex coefficients \displaystyle \{p_n\}_{n\geq 0} and \displaystyle \{q_n\}_{n\geq 0} by conditions following:

(1) For all non negative integer \displaystyle n, \displaystyle p_n and \displaystyle q_n are polynomials in \displaystyle x_0,x_1,\ldots,x_n.

(2) \displaystyle p_0=x_0 and \displaystyle q_0=1.

(3) For all positive integer \displaystyle n, \displaystyle p_n=x_0p_{n-1}(x_1,x_2,\ldots,x_n)+q_{n-1}(x_1,x_2,\ldots,x_n) and

\displaystyle q_n=p_{n-1}(x_1,x_2,\ldots,x_n).

Example. We have

\displaystyle p_1=x_0x_1+1 and \displaystyle q_1=x_1, therefore \displaystyle \frac{p_1}{q_1}=x_0+\frac{1}{x_1}.

\displaystyle p_2=x_0x_1x_2+x_0+x_2 and \displaystyle q_2=x_1x_2+1, hence

\displaystyle \frac{p_2}{q_2}=x_0+\frac{x_2}{x_1x_2+1}=x_0+\cfrac{1}{x_1+\cfrac{1}{x_2}}. \Box

For all non negative integer \displaystyle n we have

\displaystyle [x_0;x_1,x_2,\ldots,x_n]:=\frac{p_n}{q_n}=x_0+\cfrac{1}{x_1+\cfrac{1}{x_2+\cfrac{1}{x_3+\cdots+\cfrac{1}{x_{n-1}+\cfrac{1}{x_n}}}}}.

A rational function of this form is called a continued fraction.

Proposition 1. For all \displaystyle n>1, we have \displaystyle p_n=x_np_{n-1}+p_{n-2} and \displaystyle q_n=x_nq_{n-1}+q_{n-2}.

Proof. We use induction on \displaystyle n. From the above example we have the assertion is true for \displaystyle n=2. Now suppose that the assertion has been established for \displaystyle n-1 (\displaystyle n>2). Then we have

\displaystyle p_{n-1}(x_1,x_2,\ldots,x_n)=x_np_{n-2}(x_1,x_2,\ldots,x_{n-1})+p_{n-3}(x_1,x_2,\ldots,x_{n-2})

and

\displaystyle q_{n-1}(x_1,x_2,\ldots,x_n)=x_nq_{n-2}(x_1,x_2,\ldots,x_{n-1})+q_{n-3}(x_1,x_2,\ldots,x_{n-2}).

Therefore by define of \displaystyle \{p_n\} and \displaystyle \{q_n\},

\displaystyle p_n=x_0p_{n-1}(x_1,x_2,\ldots,x_n)+q_{n-1}(x_1,x_2,\ldots,x_n)=x_np_{n-1}+p_{n-2},

and \displaystyle q_n=x_nq_{n-1}+q_{n-2}. Thus the assertion is true for \displaystyle n. \Box

For convenience, we define \displaystyle p_{-2}=0, \displaystyle p_{-1}=1, \displaystyle q_{-2}=1, and \displaystyle q_{-1}=0.

Proposition 2. For all \displaystyle n>-2, we have \displaystyle p_nq_{n-1}-q_np_{n-1}=(-1)^{n-1}.

Proof. We prove by induction on \displaystyle n. The case \displaystyle n=-1 is trivial. Now suppose that the assertion is true for \displaystyle n-1 (\displaystyle n\geq 0). Then by proposition 1, we have

\displaystyle p_nq_{n-1}-q_np_{n-1}=(x_np_{n-1}+p_{n-2})q_{n-1}-(x_nq_{n-1}+q_{n-2})p_{n-1}

=-(p_{n-1}q_{n-2}-q_{n-1}p_{n-2})=(-1)^{n-1}.

Therefore the assertion is true for \displaystyle n-1. \Box

Proposition 3. For all \displaystyle n>-1, we have \displaystyle p_nq_{n-2}-q_np_{n-2}=(-1)^nx_n.

Proof. Assume \displaystyle n>-1 is an integer number. By propositions 1 and 2, we have

\displaystyle p_nq_{n-2}-q_np_{n-2}=(x_np_{n-1}+p_{n-2})q_{n-2}-(x_nq_{n-1}+q_{n-2})p_{n-2} =x_n(p_{n-1}q_{n-2}-q_{n-1}p_{n-2})=(-1)^nx_n. \Box

Proposition 4. If \displaystyle n\geq 0 and \displaystyle \theta:=[x_0;x_1,x_2,\ldots,x_{n+1}] then \displaystyle p_n-\theta q_n=\frac{(-1)^{n-1}}{q_{n+1}}.

Proof. By proposition 2, we have

\displaystyle p_n-\theta q_n=p_n-\frac{p_{n+1}}{q_{n+1}}\cdot q_n=\frac{-(p_{n+1}q_n-q_{n+1}p_n)}{q_{n+1}}=\frac{(-1)^{n-1}}{q_{n+1}}. \Box

Stern–Brocot tree


Có một dãy tương tự như dãy Farey (xem [1] và [2]), tên chúng là dãy Stern-Brocot. Dãy này được tìm ra một cách độc lập bởi Moritz Stern (1858) và Achille Brocot (1861). Stern là một nhà Toán học Đức còn Brocot là một nhà thiết kế đồng hồ người Pháp.

Trong định nghĩa sau, \displaystyle \dfrac{1}{0} là số hữu tỷ hình thức, ta xem như nó lớn hơn mọi số hữu tỷ. Dãy Stern-Brocot thứ \displaystyle n\, (n\in\mathbb{N}), ký hiệu \displaystyle SB_n, được xác định như sau: \displaystyle SB_0 là dãy \displaystyle \frac{0}{1},\frac{1}{0} và với mỗi số nguyên dương \displaystyle n, \displaystyle SB_n được tạo ra bằng cách chép lại toàn bộ (giữ nguyên thứ tự) các số hạng của \displaystyle SB_{n-1} và chèn vào giữa hai số hạng liên tiếp phân số trung gian ở dạng tối giản của chúng.

Một số dãy Stern-Brocot:

\displaystyle SB_0:\frac{0}{1},\frac{1}{0}.

\displaystyle SB_1:\frac{0}{1},\frac{1}{1},\frac{1}{0}.

\displaystyle SB_2:\frac{0}{1},\frac{1}{2},\frac{1}{1},\frac{2}{1},\frac{1}{0}.

Dễ thấy rằng với mỗi số tự nhiên \displaystyle n, \displaystyle SB_n là một dãy tăng gồm \displaystyle 2^n+1 số hữu tỷ không âm, và hai số cách đều số ở giữa là nghịch đảo của nhau.

Ta có thể nhúng các dãy Stern-Brocot vào một cây như hình , gọi là cây Stern-Brocot. Ta thấy mỗi số hữu tỷ không âm có mặt đúng một lần trong cây. Thật vậy, vì mỗi dãy Stern-Brocot là một dãy tăng nên mọi số hữu tỷ không âm xuất hiện nhiều nhất một lần trong cây, bây giờ ta chứng minh mọi số hữu tỷ không âm đều xuất hiện trong cây. Xét một số hữu tỷ không âm ở dạng tối giản \displaystyle \dfrac{m}{n}. Tồn tại số tự nhiên \displaystyle p và hai số hạng \displaystyle \dfrac{a}{b},\dfrac{a'}{b'} của \displaystyle SB_p sao cho \displaystyle \dfrac{a}{b}<\dfrac{m}{n}<\dfrac{a'}{b'}. Nếu \displaystyle \dfrac{m}{n} là phân số trung gian của \displaystyle \dfrac{a}{b},\dfrac{a'}{b'} thì tất nhiên nó xuất hiện trong cây, nếu không sẽ xảy ra một trong hai trường hợp: \displaystyle \dfrac{a}{b}<\dfrac{m}{n}<\dfrac{a+a'}{b+b'}, ta thay phân số \displaystyle \dfrac{a'}{b'} bởi \displaystyle \dfrac{a+a'}{b+b'}; \displaystyle \dfrac{a+a'}{b+b'}<\dfrac{m}{n}<\dfrac{a'}{b'}, ta thay phân số \displaystyle \dfrac{a}{b} bởi \displaystyle \dfrac{a+a'}{b+b'}. Quá trình này không thể tiếp tục mãi vì với dãy dạng \displaystyle \dfrac{a}{b}<\dfrac{m}{n}<\dfrac{a'}{b'} ta luôn có \displaystyle m+n\geq a+a'+b+b', suy ra \displaystyle \dfrac{m}{n} xuất hiện trong cây.

Khi thay \displaystyle \dfrac{0}{1}<\dfrac{1}{0} bởi hai số hữu tỷ không âm \displaystyle \dfrac{a}{b}<\dfrac{c}{d} với \displaystyle bc-ad=1 ta sẽ được các dãy mới, gọi là các dãy Stern-Brocot suy rộng. Có thể chứng minh được rằng mọi số hữu tỷ nằm giữa \displaystyle \dfrac{a}{b} và \displaystyle \dfrac{c}{d} đều xuất hiện trong một dãy Stern-Brocot suy rộng nào đó.

Đọc thêm

[1] https://nttuan.org/2008/04/02/farey-sequence-and-approximation-of-irrational-numbers-i/

[2] https://nttuan.org/2008/05/02/farey-sequence-and-approximation-of-irrational-numbers-ii/

Farey sequence and approximation of irrational numbers II


Đây là phần II, các bạn xem lại phần I ở đây https://nttuan.org/2008/04/02/farey-sequence-and-approximation-of-irrational-numbers-i/

Bây giờ chúng tôi sẽ sử dụng các dãy Farey để chứng minh lại một số kết quả về xấp xỉ số vô tỷ bởi số hữu tỷ (xem thêm [1]).

Định lý 4 (Dirichlet, 1842). Cho số vô tỷ \displaystyle \alpha. Khi đó có vô hạn phân số tối giản \displaystyle \frac{a}{q} sao cho

\displaystyle \left|\alpha-\frac{a}{q}\right|<\frac{1}{q^2}. Hơn nữa ta có thể chọn \displaystyle q lớn tùy ý.

Chứng minh. Không mất tính tổng quát ta giả sử \displaystyle 0<\alpha<1. Ta có thể chọn \displaystyle a=0,q=1 để được một phân số tối giản thỏa mãn. Giả sử ta đã xây dựng được một vài phân số, ta sẽ chỉ ra một phân số khác cũng thỏa mãn bất đẳng thức trong định lý nhưng khác tất cả các phân số này. Chọn số nguyên dương \displaystyle n đủ lớn sao cho \displaystyle \frac{1}{n} nhỏ hơn tất cả các khoảng cách từ \displaystyle \alpha đến các phân số đã được tìm. Số \displaystyle \alpha sẽ nằm giữa hai phần số liên tiếp \displaystyle a/b<c/d của \displaystyle F_n, giả sử \displaystyle b\geq d. Vì \displaystyle \frac{c}{d}-\dfrac{a}{b}=\frac{1}{bd}\leq\frac{1}{b+d-1}\leq\frac{1}{n} nên cả \displaystyle a/b và \displaystyle c/d đều khác tất cả các phân số trước, mà \displaystyle |\alpha-c/d|<\frac{1}{bd}<\frac{1}{d^2}, suy ra ta có thể chọn $c/d$ là phân số tiếp theo. \Box

Định lý 5 (Hurwitz, 1891). Cho số vô tỷ \displaystyle \alpha. Khi đó có vô hạn phân số tối giản \displaystyle \frac{a}{q} sao cho

\displaystyle \left|\alpha-\frac{a}{q}\right|<\frac{1}{\sqrt{5}q^2}. Hơn nữa ta có thể chọn \displaystyle q lớn tùy ý. Với số thực \displaystyle A>\sqrt{5}, chỉ có hữu hạn phân số tối giản \displaystyle \dfrac{a}{q} sao cho

\displaystyle \left|\alpha-\frac{a}{q}\right|<\frac{1}{Aq^2}, ở đây \displaystyle \alpha=\dfrac{\sqrt{5}-1}{2}.

Chứng minh. Không mất tính tổng quát ta giả sử \displaystyle 0<\alpha<1. Xét một số nguyên dương \displaystyle n bất kỳ. Số \displaystyle \alpha sẽ nằm giữa hai phần số liên tiếp \displaystyle a/b<c/d của \displaystyle F_n. Ta chỉ cần chứng minh một trong ba phân số \displaystyle \frac{a}{b}, \displaystyle \frac{c}{d}, và \displaystyle \frac{a+c}{b+d} thỏa mãn bất đẳng thức trong định lý, phần sau sẽ làm như trong chứng minh định lý 4. Giả sử \displaystyle \frac{a}{b}<\frac{a+c}{b+d}<\alpha<\frac{c}{d} và cả ba phân số đều không thỏa mãn bất đẳng thức trong định lý, nghĩa là

\displaystyle \alpha-\frac{a}{b}\geq \frac{1}{\sqrt{5}b^2},\quad\alpha-\frac{a+c}{b+d}\geq\frac{1}{\sqrt{5}(b+d)^2},\quad \frac{c}{d}-\alpha\geq\frac{1}{\sqrt{5}d^2}. Cộng theo vế bất đẳng thức thứ nhất với thứ ba, thứ hai với thứ ba ta được \displaystyle \frac{\sqrt{5}}{bd}\geq\frac{1}{b^2}+\frac{1}{d^2},\quad \frac{\sqrt{5}}{d(b+d)}\geq \frac{1}{(b+d)^2}+\frac{1}{d^2}. Đặt \displaystyle b/d=t, từ trên ta có một hệ bất phương trình bậc hai ẩn \displaystyle t, giải hệ này ta có \displaystyle t=\dfrac{\sqrt{5}-1}{2}\not\in\mathbb{Q}, vô lí.

Với phần thứ hai, giả sử bất đẳng thức đúng với vô hạn phân số \displaystyle a/q. Vì mỗi \displaystyle q chỉ có nhiều nhất hai giá trị \displaystyle a làm cho bất đẳng thức đó đúng nên \displaystyle q chạy trên một tập vô hạn. Viết lại bất đẳng thức trong định lý dưới dạng

\displaystyle \frac{q\sqrt{5}}{2}-\frac{1}{Aq}<\frac{q}{2}+a<\frac{q\sqrt{5}}{2}+\frac{1}{Aq}, bình phương ta có \displaystyle \frac{1}{A^2q^2}-\frac{\sqrt{5}}{A}<a^2+aq-q^2<\frac{1}{A^2q^2}+\frac{\sqrt{5}}{A}. Vì \displaystyle A>\sqrt{5} nên ta có thể chọn \displaystyle q đủ lớn để

\displaystyle -1<\frac{1}{A^2q^2}-\frac{\sqrt{5}}{A}<a^2+aq-q^2<\frac{1}{A^2q^2}+\frac{\sqrt{5}}{A}<1, với q này thì a^2+aq-q^2=0, vô lý. \Box

Đọc thêm

[1] https://nttuan.org/2007/12/15/pell-equation/

Farey sequence and approximation of irrational numbers I


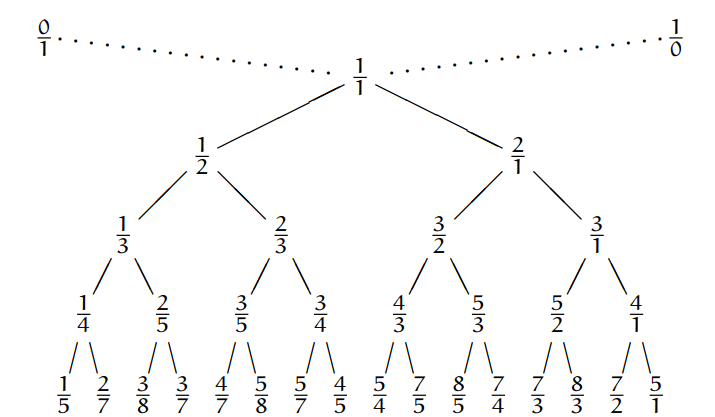
Trong bài này chúng ta sẽ tìm hiểu về các dãy Farey. Phần đầu là kiến thức cơ bản về dãy Farey, ở phần thứ hai chúng ta sẽ dùng dãy Farey để chứng minh lại một số định lý xấp xỉ (xem [1]).

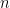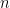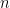Cho số nguyên dương \displaystyle n. Phân số tối giản \displaystyle \frac{p}{q}\in [0;1] được gọi là phân số Farey bậc \displaystyle n nếu \displaystyle 0<q\leq n. Dãy tăng tất cả các phân số Farey bậc \displaystyle n được gọi là dãy Farey bậc 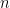\displaystyle n,  ký hiệu là \displaystyle F_n.

Bốn dãy Farey đầu tiên là: 

\displaystyle \displaystyle F_1:\,\frac{0}{1};\frac{1}{1}.

\displaystyle \displaystyle F_2:\,\frac{0}{1};\frac{1}{2};\frac{1}{1}.

\displaystyle \displaystyle F_3:\,\frac{0}{1};\frac{1}{3};\frac{1}{2};\frac{2}{3};\frac{1}{1}.

\displaystyle \displaystyle F_4:\,\frac{0}{1};\frac{1}{4};\frac{1}{3};\frac{1}{2};\frac{2}{3};\frac{3}{4};\frac{1}{1}.

Rõ ràng là với mỗi số nguyên dương 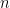\displaystyle n, dãy \displaystyle F_n có đúng \displaystyle 1+\sum_{k=1}^n\varphi (k) số hạng.

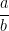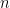Định lý 1. Cho các số tự nhiên \displaystyle a,b,c và \displaystyle d thỏa mãn \displaystyle 0\leq \frac{a}{b}<\frac{c}{d}\leq 1 và \displaystyle bc-ad=1. Khi đó \displaystyle \frac{a}{b} và \displaystyle \frac{c}{d} là hai số hạng liên tiếp của dãy \displaystyle F_n. Ở đây \displaystyle n là một số nguyên dương thỏa mãn \displaystyle \max\{b,d\}\leq n\leq b+d-1.

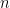Chứng minh. Từ \displaystyle bc-ad=1 ta có \displaystyle \displaystyle \frac{a}{b},\frac{c}{d} là hai phân số tối giản, mà \displaystyle \max\{b,d\}\leq n, suy ra chúng là các số hạng của dãy \displaystyle F_n. Nếu chúng không phải là hai số hạng liên tiếp của \displaystyle F_n thì tồn tại phân số Farey bậc \displaystyle n, ký hiệu là \displaystyle \frac{h}{k}, thỏa mãn \displaystyle \frac{a}{b}<\frac{h}{k}<\frac{c}{d}. Vì \displaystyle ck-dh\geq 1 và \displaystyle bh-ak\geq 1 nên

\displaystyle b+d-1\geq n\geq k=(bc-ad)k=b(ck-dh)+d(bh-ak)\geq b+d,

đây là điều không thể xảy ra. \Box

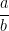Với các số tự nhiên \displaystyle a,b,c và \displaystyle d thỏa mãn \displaystyle 0\leq \frac{a}{b}<\frac{c}{d}, phân số \displaystyle \dfrac{a+c}{b+d} được gọi là phân số trung gian của hai phân số \displaystyle \frac{a}{b} và \displaystyle \frac{c}{d}. Từ chứng minh trên ta có:

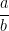Định lý 2. Cho các số tự nhiên \displaystyle a,b,c và \displaystyle d thỏa mãn \displaystyle 0\leq \frac{a}{b}<\frac{c}{d}\leq 1 và \displaystyle bc-ad=1. Khi đó nếu \displaystyle \dfrac{h}{k} là phân số trung gian của hai phân số \displaystyle \frac{a}{b}, \displaystyle \frac{c}{d} thì \displaystyle \frac{a}{b}<\frac{h}{k}<\frac{c}{d} và \displaystyle bh-ak=1,\quad ck-dh=1.

Từ kết quả này ta thấy trong định lý 1, nếu \displaystyle n>b+d-1 thì \displaystyle a/b và \displaystyle c/d không phải là hai số hạng liên tiếp của \displaystyle F_n. Định lý sau cho một cách xác định các dãy Farey bằng quy nạp.

Định lý 3. Với mọi số nguyên dương 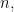n, ta có

(1) Dãy \displaystyle F_{n+1} có được từ dãy \displaystyle F_n bằng cách viết vào giữa hai số hạng liên tiếp của \displaystyle F_n có tổng các mẫu không vượt quá \displaystyle n+1 phân số trung gian của chúng.

(2) Nếu \displaystyle \frac{a}{b}<\frac{c}{d} là hai số hạng liên tiếp của \displaystyle F_n thì \displaystyle bc-ad=1.

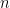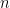Chứng minh. Ta sẽ chứng minh bằng quy nạp theo \displaystyle n. Rõ ràng khẳng định đúng với \displaystyle n=1. Giả sử khẳng định đúng với các số nguyên dương bé hơn \displaystyle n\, (n\geq 2), ta sẽ chứng minh khẳng định đúng với \displaystyle n. Từ các kết quả trước và giả thiết quy nạp ta có nếu \displaystyle \frac{a}{b}<\frac{c}{d} là hai số hạng liên tiếp của \displaystyle F_n thì \displaystyle bc-ad=1. Sau khi viết vào giữa hai số hạng liên tiếp của \displaystyle F_n có tổng các mẫu không vượt quá \displaystyle n+1 phân số trung gian của chúng ta thu được dãy con \displaystyle F^{\prime}_n của \displaystyle F_{n+1}. Nếu trong \displaystyle F_{n+1} có phân số \displaystyle \dfrac{h}{k} không thuộc \displaystyle F'_n thì tồn tại hai số hạng liên tiếp \displaystyle \frac{a}{b}<\frac{c}{d} của \displaystyle F'_n sao cho \displaystyle \frac{a}{b}<\frac{h}{k}<\frac{c}{d}. Vì \displaystyle \frac{h}{k} không thuộc \displaystyle F^{\prime}_n nên nó cũng không thuộc \displaystyle F_n, suy ra \displaystyle k>n, kết hợp với \displaystyle k\leq n+1 ta có \displaystyle k=n+1. 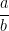Từ chứng minh của các kết quả trên suy ra \displaystyle k=n+1\geq b+d, do đó \displaystyle \frac{a}{b} và \displaystyle \frac{c}{d} là hai phân số liên tiếp của \displaystyle F_n. Mà \displaystyle b+d\leq n+1, suy ra chúng không thể là hai số hạng liên tiếp của \displaystyle F^{\prime}_n, vô lý. \Box

Dãy số Farey được đặt theo tên của nhà địa chất người Anh John Farey, lá thư của ông về những dãy này đã được đăng vào năm 1816. Farey phỏng đoán, mà không đưa ra chứng minh, rằng mỗi số hạng trong một dãy Farey là trung gian của các số liên tiếp trong dãy Farey ngay trước nó. Bức thư của Farey đã được đọc bởi Cauchy, người đã đưa ra chứng minh trong một cuốn sách của mình và cho rằng kết quả này là của Farey. Trên thực tế, một nhà toán học khác, Charles Haros, đã công bố những kết quả tương tự vào năm 1802 mà cả Farey và Cauchy đều không biết. Vì vậy, đó là một sự tình cờ lịch sử đã liên kết tên tuổi của Farey với những dãy này. Một lần nữa, trước đó là Pell, người có tên được đặt cho một mối quan hệ toán học không phải là người đầu tiên tìm ra nó.

Đọc thêm

[1] https://nttuan.org/2007/12/15/pell-equation/