Bài này là một mở đầu của phương pháp sàng trong các bài toán đếm. Ở phương pháp này, khi muốn đếm số phần tử của một tập  , ta bắt đầu với một tập
, ta bắt đầu với một tập 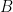 chứa
chứa  , sau đó tìm cách loại đi các phần tử không nằm trong
, sau đó tìm cách loại đi các phần tử không nằm trong  .
.
Để theo dõi bài này cho dễ, các bạn hãy xem qua các bài sau:
[1] https://nttuan.org/2011/09/15/basic-counting-principles/
[2] https://nttuan.org/2012/09/15/permutations/
[3] https://nttuan.org/2013/09/15/combinations/
Chúng ta biết rằng nếu  và
và 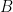 là các tập hữu hạn rời nhau thì
là các tập hữu hạn rời nhau thì  , tổng quát hơn ta có: Nếu
, tổng quát hơn ta có: Nếu  và
và 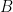 là các tập hữu hạn bất kỳ thì
là các tập hữu hạn bất kỳ thì  đây chính là nguyên lý bù-trừ cho hai tập hợp. Với
đây chính là nguyên lý bù-trừ cho hai tập hợp. Với 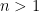 tập hợp ta có định lí sau
tập hợp ta có định lí sau
Định lí. Nếu 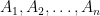 là các tập hữu hạn thì
là các tập hữu hạn thì

Chứng minh. Ta sẽ chứng minh rằng mỗi phần tử trong  được đếm đúng một lần trong vế phải. Gọi
được đếm đúng một lần trong vế phải. Gọi  là một phần tử trong hợp đó và nó nằm trong dúng
là một phần tử trong hợp đó và nó nằm trong dúng  tập
tập 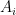 , khi đó trong vế phải nó sẽ được đếm đúng
, khi đó trong vế phải nó sẽ được đếm đúng  lần (lưu ý
lần (lưu ý  ).
). 
Ngoài cách chứng minh trên các bạn có thể chứng minh định lí bằng phương pháp quy nạp toán học, tôi chọn giới thiệu cách chứng minh này vì phong cách tổ hợp của nó.
Ví dụ 1. Có bao nhiêu số nguyên dương  sao cho
sao cho  là ước của ít nhất một trong hai số
là ước của ít nhất một trong hai số  và
và  ?
?
Lời giải. Gọi  và
và 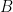 lần lượt là tập các ước dương của
lần lượt là tập các ước dương của  và
và  . Đề bài yêu cầu tính
. Đề bài yêu cầu tính  . Ta có
. Ta có  và
và  Suy ra
Suy ra  và
và  Bởi thế nên
Bởi thế nên 

Ví dụ 2. Tìm số các số nguyên dương trong  chia hết cho
chia hết cho  hoặc
hoặc  hoặc
hoặc 
Lời giải. Đặt  . Gọi
. Gọi  và
và 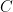 lần lượt là tập các phần tử của
lần lượt là tập các phần tử của  chia hết cho
chia hết cho  và
và  . Khi đó
. Khi đó  là tập các số nguyên dương trong
là tập các số nguyên dương trong  chia hết cho
chia hết cho  hoặc
hoặc  hoặc
hoặc  Đề bài yêu cầu tính
Đề bài yêu cầu tính  .
.
Vì  và
và  là các số nguyên dương đôi một nguyên tố cùng nhau nên
là các số nguyên dương đôi một nguyên tố cùng nhau nên  là tập các số nguyên dương trong
là tập các số nguyên dương trong  chia hết cho
chia hết cho 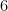 ,
,  là tập các số nguyên dương trong
là tập các số nguyên dương trong  chia hết cho
chia hết cho  ,
,  là tập các số nguyên dương trong
là tập các số nguyên dương trong  chia hết cho
chia hết cho 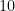 , và
, và  là tập các số nguyên dương trong
là tập các số nguyên dương trong  chia hết cho
chia hết cho  . Suy ra
. Suy ra 
![\displaystyle=\left[\frac{500}{2}\right]+\left[\frac{500}{3}\right]+\left[\frac{500}{5}\right]-\left[\frac{500}{6}\right]-\left[\frac{500}{15}\right]-\left[\frac{500}{10}\right]+\left[\frac{500}{30}\right]=366.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle%3D%5Cleft%5B%5Cfrac%7B500%7D%7B2%7D%5Cright%5D%2B%5Cleft%5B%5Cfrac%7B500%7D%7B3%7D%5Cright%5D%2B%5Cleft%5B%5Cfrac%7B500%7D%7B5%7D%5Cright%5D-%5Cleft%5B%5Cfrac%7B500%7D%7B6%7D%5Cright%5D-%5Cleft%5B%5Cfrac%7B500%7D%7B15%7D%5Cright%5D-%5Cleft%5B%5Cfrac%7B500%7D%7B10%7D%5Cright%5D%2B%5Cleft%5B%5Cfrac%7B500%7D%7B30%7D%5Cright%5D%3D366.&bg=ffffff&fg=000000&s=0&c=20201002)

Với mỗi số nguyên dương  , ký hiệu
, ký hiệu  là số các số nguyên dương không vượt quá
là số các số nguyên dương không vượt quá  và nguyên tố cùng nhau với
và nguyên tố cùng nhau với  . Hàm số
. Hàm số  được gọi là hàm phi của Euler.
được gọi là hàm phi của Euler.
Ví dụ 3. Tính  .
.
Lời giải. Vì  nên
nên 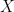 chính là tập các số trong
chính là tập các số trong  không chia hết cho
không chia hết cho  và
và  . Suy ra
. Suy ra  với
với  là tập các số trong
là tập các số trong  chia hết cho
chia hết cho  ,
, 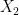 là tập các số trong
là tập các số trong  chia hết cho
chia hết cho  , và
, và  là tập các số trong
là tập các số trong  chia hết cho
chia hết cho  Tương tự như bài toán trên ta có
Tương tự như bài toán trên ta có

![\displaystyle =\left[\frac{180}{2}\right]+\left[\frac{180}{3}\right]+\left[\frac{180}{5}\right]-\left[\frac{180}{6}\right]-\left[\frac{180}{15}\right]-\left[\frac{180}{10}\right]+\left[\frac{180}{30}\right]=132.](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle+%3D%5Cleft%5B%5Cfrac%7B180%7D%7B2%7D%5Cright%5D%2B%5Cleft%5B%5Cfrac%7B180%7D%7B3%7D%5Cright%5D%2B%5Cleft%5B%5Cfrac%7B180%7D%7B5%7D%5Cright%5D-%5Cleft%5B%5Cfrac%7B180%7D%7B6%7D%5Cright%5D-%5Cleft%5B%5Cfrac%7B180%7D%7B15%7D%5Cright%5D-%5Cleft%5B%5Cfrac%7B180%7D%7B10%7D%5Cright%5D%2B%5Cleft%5B%5Cfrac%7B180%7D%7B30%7D%5Cright%5D%3D132.&bg=ffffff&fg=000000&s=0&c=20201002) Do đó
Do đó 

Làm tương tự như trên ta có nếu  có phân tích chính tắc
có phân tích chính tắc  thì
thì 
Ví dụ 4. Tìm số các lời giải nguyên không âm của phương trình  với
với  và
và  .
.
Lời giải. Gọi  là tập các nghiệm nguyên không âm của phương trình
là tập các nghiệm nguyên không âm của phương trình  và
và 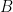 là tập các nghiệm nguyên không âm của phương trình thỏa mãn
là tập các nghiệm nguyên không âm của phương trình thỏa mãn  và
và  Ta cần tính
Ta cần tính  Ta có
Ta có  trong đó:
trong đó: 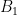 là tập các nghiệm nguyên không âm của phương trình thỏa mãn
là tập các nghiệm nguyên không âm của phương trình thỏa mãn 
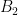 là tập các nghiệm nguyên không âm của phương trình thỏa mãn
là tập các nghiệm nguyên không âm của phương trình thỏa mãn 
 là tập các nghiệm nguyên không âm của phương trình thỏa mãn
là tập các nghiệm nguyên không âm của phương trình thỏa mãn 
Theo nguyên lý bù-trừ, ta có 
Bộ số tự nhiên 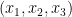 thuộc
thuộc 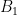 khi và chỉ khi
khi và chỉ khi  do đó
do đó  Hoàn toàn tương tự, ta có
Hoàn toàn tương tự, ta có  và
và 
Bộ số tự nhiên 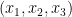 thuộc
thuộc  khi và chỉ khi
khi và chỉ khi  do đó
do đó  Hoàn toàn tương tự, ta có
Hoàn toàn tương tự, ta có 
 và
và 
Bây giờ thay các kết quả trên vào  ta có
ta có 

Ví dụ 5. Tìm số nghiệm nguyên của phương trình  với
với  và
và  .
.
Hướng dẫn. Đáp số:  Đặt
Đặt 
 và
và  Ta cần tính số nghiệm tự nhiên của phương trình
Ta cần tính số nghiệm tự nhiên của phương trình  thỏa mãn
thỏa mãn 
 và
và  Đến đây làm như ví dụ trên.
Đến đây làm như ví dụ trên. 
Ví dụ 6. Với  cho
cho 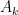 là một tập với
là một tập với 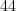 phần tử. Giả sử rằng
phần tử. Giả sử rằng  với mỗi
với mỗi  khác nhau trong
khác nhau trong  Tính
Tính 
Hướng dẫn. Chứng minh giao của tất cả các tập chứa đúng một phần tử. Từ đó có đáp số là 
Cuối cùng là một áp dụng quan trọng của nguyên lý bù-trừ vào bài toán Bernoulli-Euler về các bức thư sai địa chỉ.
Continue reading “Principle of inclusion and exclusion” →