Bipartite graph

Một đồ thị $G$ được gọi là hai phần (hay lưỡng phân) nếu $V(G)$ có thể phân hoạch thành hai tập con $X$ và $Y$ , sao cho mỗi phần tử của $E(G)$ có một đầu mút trong $X$ và đầu mút còn lại trong $Y$ . Khi đó $X$ và $Y$ được gọi là các phần của đồ thị lưỡng phân. Ta ký hiệu đồ thị lưỡng phân với hai phần $X$ và $Y$ bởi $G[X,Y]$ . Nếu trong $G[X,Y]$ , mọi đỉnh thuộc $X$ được nối với mọi đỉnh của $Y$ thì $G[X,Y]$ được gọi là đồ thị lưỡng phân đầy đủ.

Ví dụ 1. Gọi $X$ và $Y$ lần lượt là tập các cầu thủ bóng đá và tập các câu lạc bộ trong một thành phố. Khi đó ta có đồ thị lưỡng phân $G[X,Y]$ , ở đây $x\in X$ được nối với $y\in Y$ khi và chỉ khi $x$ đã từng chơi cho $y$ .

Ví dụ 2 (Bài toán tối ưu trong đường sắt). Giả sử ta có một lịch trình các chuyến tàu cùng các điểm dừng của chúng, và cần tìm một tập hợp các ga tàu càng nhỏ càng tốt sao cho mọi chuyến tàu ghé thăm ít nhất một trong các ga đã chọn. Bài toán này có thể được mô hình hóa như một bài toán trên đồ thị lưỡng phân có các phần là tập các chuyến tàu và tập các ga tàu, mỗi chuyến tàu nối với ga mà nó sẽ dừng.

Bây giờ chúng tôi sẽ giới thiệu một số kết quả cơ bản về đồ thị hai phần.

Định lý 1. Cho đồ thị lưỡng phân $G[X,Y]$ không có đỉnh cô lập và thỏa mãn $\deg (x)\geq \deg (y)$ với mọi $xy\in E(G)$ ( $x\in X$ và $y\in Y$ ). Khi đó $\mid X\mid \leq \mid Y\mid$ . Đẳng thức xảy ra khi và chỉ khi $\deg (x)= \deg (y)$ với mọi $xy\in E(G)$ ( $x\in X$ và $y\in Y$ ).

Chứng minh. Vì $G$ không có đỉnh cô lập nên với mỗi $(x,y)\in X\times Y$ , ta có

$\displaystyle \sum_{y^{\prime}\in N(x)}\frac{1}{\deg (x)}=\sum_{x^{\prime}\in N(y)}\frac{1}{\deg (y)}=1.$

Suy ra

$\displaystyle \mid X\mid =\sum_{x\in X}\sum_{y\in N(x)}\frac{1}{\deg (x)}=\sum_{\substack{(x,y)\in X\times Y\\ xy\in E(G)}}\frac{1}{\deg x},$

và

$\displaystyle \mid Y\mid =\sum_{y\in Y}\sum_{x\in N(y)}\frac{1}{\deg (y)}=\sum_{\substack{(x,y)\in X\times Y\\ xy\in E(G)}}\frac{1}{\deg y}.$

Kết hợp với giả thiết $\deg (x)\geq \deg (y)$ với mọi $xy\in E(G)$ ( $x\in X$ và $y\in Y$ ) ta có những điều cần chứng minh. $\Box$

Định lý 2. Một đồ thị là lưỡng phân khi và chỉ khi nó không chứa chu trình độ dài lẻ.

Chứng minh. Nếu một đồ thị là lưỡng phân thì dọc theo một chu trình của nó, các đỉnh thuộc hai phần sẽ xuất hiện luân phiên. Vì thế, mỗi chu trình trong đồ thị lưỡng phân phải có độ dài là số chẵn. Bây giờ xét một đồ thị $G$ không chứa chu trình với độ dài là số lẻ. Ta chỉ cần xét tình huống $G$ là một đồ thị liên thông.

Gọi $T$ là một cây bao trùm trong $G$ (nó tồn tại theo [1]), và chọn một đỉnh $r$ làm gốc của cây này. Gọi $C$ là tập tất cả các đỉnh mà đường đi trong $T$ nối $r$ với nó có độ dài chẵn, và $L$ là tập tất cả các đỉnh mà đường đi trong $T$ nối $r$ với nó có độ dài chẵn. Khi đó $V(G)$ được phân hoạch thành hai phần $C$ và $L$ .

Ta sẽ chứng minh $G$ là đồ thị lưỡng phân với các phần là $L$ và $C$ . Xét hai đỉnh kề nhau $x$ và $y$ của $G$ . Nếu $xy\in T$ thì độ dài của $rTx$ và độ dài của $rTy$ khác tính chẵn-lẻ, do đó trong hai đỉnh $x$ , $y$ có một đỉnh thuộc $C$ và đỉnh còn lại thuộc $L$ . Nếu $xy\not \in T$ , từ giả thiết ta thấy chu trình $xTy\cup xy$ có độ dài chẵn. Theo phần chứng minh trước thì mỗi cạnh khác $xy$ thuộc chu trình này có các đầu mút thuộc hai phần khác nhau của phân hoạch, suy ra $x$ và $y$ thuộc hai phần khác nhau của phân hoạch. $\Box$

Tài liệu tham khảo

[1] https://nttuan.org/2024/08/02/tree/

Discrete random variables

Ta thường không quan tâm đến thí nghiệm mà chỉ quan tâm đến một số hệ quả từ thí nghiệm đó. Chẳng hạn, những tay cờ bạc chỉ quan tâm đến số tiền họ được hay mất, không quan tâm mấy đến trò chơi. Nhiều hệ quả từ thí nghiệm có thể được biểu diễn bằng một hàm trên không gian mẫu của thí nghiệm.

Định nghĩa 1. Cho một không gian xác suất $(\Omega,\mathcal{F},\mathbb{P})$ . Một biến ngẫu nhiên là một hàm $X:\Omega\to\mathbb{R}$ sao cho với mỗi $x\in\mathbb{R}$ , $\{\omega\in\Omega\mid X(\omega)\leq x\}\in\mathcal{F}.$

Một biến ngẫu nhiên được gọi là rời rạc nếu nó chỉ nhận giá trị trong một tập hợp đếm được.

Không khó khăn lắm để thấy rằng nếu $X$ và $Y$ là các biến ngẫu nhiên (biến ngẫu nhiên rời rạc) thì $X+Y$ , $XY$ , và $\alpha X$ ( $\alpha\in\mathbb{R}$ ) cũng là các biến ngẫu nhiên (biến ngẫu nhiên rời rạc).

Định nghĩa 2. Cho một không gian xác suất $(\Omega,\mathcal{F},\mathbb{P})$ và một biến ngẫu nhiên $X:\Omega\to\mathbb{R}$ . Hàm phân bố của biến ngẫu nhiên $X$ là hàm $F_X:\mathbb{R}\to [0;1]$ xác định bởi

$F_X(x)=\mathbb{P}(\{\omega\in\Omega\mid X(\omega)\leq x\}),\quad\forall x\in\mathbb{R}.$

Để cho gọn, ta viết sự kiện $\{\omega\in\Omega\mid X(\omega)\leq x\}$ bởi $\{ X\leq x\}$ . Khi đó xác suất $\mathbb{P}(\{\omega\in\Omega\mid X(\omega)\leq x\})$ sẽ được viết là $\mathbb{P}( X\leq x)$ .

Ví dụ 1. Tung một đồng xu hai lần. Không gian mẫu của phép thử là $\Omega =\{NN,SS,SN,NS\}$ . Xét biến ngẫu nhiên $X$ , số mặt ngửa, xác định bởi

$X(NN)=2, X(SS)=0, X(SN)=1, X(NS)=1.$

Hàm phân bố của $F_X:\mathbb{R}\to [0;1]$ của $X$ xác định bởi

$F_X(x)=\begin{cases}0,\quad x<0\\ 1/4,\quad 0\leq x<1\\ 3/4,\quad 1\leq x<2\\ 1,\quad x\geq 2.\end{cases}$

Ví dụ 2. Xét không gian xác suất $(\Omega,\mathcal{F},\mathbb{P})$ và một biến cố $A$ . Hàm chỉ báo của $A$ là hàm $I_A: \Omega\to \mathbb{R}$ xác định bởi

$I_A(\omega)=\begin{cases}1,\quad \omega\in A\\ 0,\quad \omega\not\in A.\end{cases}$

Ta thấy $I_A$ là một biến ngẫu nhiên rời rạc với hàm phân bố $F:\mathbb{R}\to [0;1]$ xác định bởi

$F(x)=\begin{cases}0,\quad x<0\\ 1-\mathbb{P}(A),\quad 0\leq x<1\\ 1,\quad x\geq 1. \end{cases}$

Nếu $\{A_i\}_{i\in I}$ là một họ các biến cố đôi một rời nhau sao cho $\displaystyle A\subset \bigcup_{i\in I} A_i$ thì

$I_A(\omega)=\sum_{i\in I}I_{A\cap A_i}(\omega),\quad \forall \omega\in \Omega.$ $\Box$

Định lý 1. Hàm phân bố $F_X$ của biến ngẫu nhiên $X$ có các tính chất sau

(a) với mỗi số thực $x_1$ và $x_2$ , nếu $x_1<x_2$ thì $F_X(x_1)\leq F_X(x_2)$ .

(b) $\displaystyle \lim_{x\to -\infty}F_X(x)=0$ và $\displaystyle \lim_{x\to +\infty}F_X(x)=1$ .

(c) $F_X$ liên tục phải tại mọi điểm.

Chứng minh. Xét hai số thực $x_1$ và $x_2$ với $x_1<x_2$ . Biến cố $\{X\leq x_2\}$ là hợp của hai biến cố rời nhau $\{X\leq x_1\}$ và $\{x_1<X\leq x_2\}$ nên

$F_X(x_2)=\mathbb{P}(X\leq x_2)=\mathbb{P}(X\leq x_1)+\mathbb{P}(x_1<X\leq x_2)\geq \mathbb{P}(X\leq x_1)=F_X(x_1).$

Ta có $\{X\leq n\}_{n\geq 1}$ là một dãy tăng các sự kiện có hợp bằng $\Omega$ , theo định lý 1 trong [1], ta có

$1=\mathbb{P}(\Omega)=\mathbb{P}\left(\bigcup_{n=1}^{+\infty}\{X\leq n\}\right)=\lim_{n\to +\infty}\mathbb{P}(X\leq n),$

kết hợp với tính đơn điệu của $F_X$ ta được $\displaystyle \lim_{x\to +\infty}F_X(x)=1$ . Tính chất $\displaystyle \lim_{x\to -\infty}F_X(x)=0$ được chứng minh theo cách tương tự.

Bây giờ xét một số thực $x_0$ . Ta thấy $\{x_0<X\leq x_0+\frac{1}{n}\}_{n\geq 1}$ là một dãy giảm các sự kiện có giao bằng rỗng, theo định lý 2 trong [1], ta có

$0=\mathbb{P}\left(\bigcap_{n=1}^{+\infty}\left\{x_0<X\leq x_0+\frac{1}{n}\right\}\right)=\lim_{n\to +\infty}\left(F_X\left(x_0+\frac{1}{n}\right)-F_X(x_0)\right),$

kết hợp với tính đơn điệu của $F_X$ ta có $F_X$ liên tục phải tại $x_0$ . $\Box$

Continue reading →

Tree

Một đồ thị không chứa chu trình được gọi là một rừng. Một rừng liên thông được gọi là một cây.

Ví dụ 1. Cho $G$ là một cây trên $n>1$ đỉnh. Chứng minh rằng $G$ có ít nhất hai lá, và nếu $v$ là một lá thì $G\setminus\{v\}$ là một cây.

Hướng dẫn. Trong các đường đi của $G$ , quan tâm đến một đường đi dài nhất. Chứng minh hai đầu của nó là lá. Chỉ ra $G\setminus\{v\}$ là một rừng liên thông. $\Box$

Định lý 1. Với một đồ thị $G$ , các khẳng định sau là tương đương:

(1) $G$ là một cây;

(2) Mỗi hai đỉnh của $G$ được nối với nhau bởi một đường đi duy nhất trong $G$ ;

(3) $G$ là đồ thị liên thông và với mỗi cạnh $e$ , đồ thị có được từ $G$ bằng cách bỏ đi cạnh $e$ không phải là đồ thị liên thông;

(4) $G$ không chứa chu trình và với mỗi hai đỉnh không kề nhau $x$ và $y$ , đồ thị có được từ $G$ bằng cách thêm vào cạnh $xy$ chứa một chu trình.

Chứng minh. Giả sử $G$ là một cây và $x$ , $y$ là hai đỉnh của $G$ . Vì $G$ là đồ thị liên thông nên có một đường đi nối $x$ và $y$ , ký hiệu là $\alpha$ . Nếu có một đường đi khác đường đi này nối $x$ và $y$ , ký hiệu là $\beta$ , gọi $z$ là đỉnh chung gần $x$ nhất của hai đường đi. Đường đi từ $x$ đến $z$ dọc theo $\alpha$ hợp với đường đi từ $z$ đến $x$ dọc theo $\beta$ tạo thành một chu trình, vô lý. Vậy ta đã chứng minh $(1)\Rightarrow (2)$ .

Xét một cạnh $e=xy$ của $G$ . Nếu đồ thị có được từ $G$ bằng cách bỏ đi cạnh $e$ là đồ thị liên thông, thì trong $G$ có một đường đi nối $x$ và $y$ mà không chứa $e$ . Đường đi này cùng với $e$ là hai đường đi nối $x$ và $y$ . Vậy ta đã chứng minh $(2)\Rightarrow (3)$ , vì nếu có $(2)$ thì đồ thị phải là đồ thị liên thông.

Bây giờ giả sử có $(3)$ . Trước tiên ta thấy $G$ không chứa chu trình, vì nếu không ta bỏ đi một cạnh của chu trình thì đồ thị mới vẫn liên thông, vô lý. Xét hai đỉnh không kề nhau $x$ và $y$ . Vì $G$ là đồ thị liên thông nên có đường đi nối $x$ và $y$ . Thêm cạnh $xy$ vào đường đi này ta có một chu trình trong đồ thị có được từ $G$ bằng cách thêm vào cạnh $xy$ . Vậy ta có $(4)$ .

Cuối cùng, ta giả sử có $(4)$ . Xét hai đỉnh phân biệt $x$ và $y$ . Nếu $x$ và $y$ kề nhau thì có đường đi nối $x$ và $y$ , là $xy$ chẳng hạn. Nếu $x$ và $y$ không kề nhau thì đồ thị có được từ $G$ bằng cách thêm vào cạnh $xy$ chứa một chu trình. Vì $G$ không chứa chu trình nên chu trình này chứa $xy$ , bỏ $xy$ ra khỏi nó ta có đường đi trong $G$ nối $x$ và $y$ . Vậy ta có $(1)$ . $\Box$

Hệ quả. Một đồ thị liên thông trên $n$ đỉnh là một cây khi và chỉ khi nó có $n-1$ cạnh.

Chứng minh. Giả sử $G$ là một cây trên $n$ đỉnh. Vì $G$ là đồ thị liên thông nên theo định lý 1 trong [4], ta có thể đánh số các đỉnh của $G$ là $v_1$ , $v_2$ , $\ldots$ , $v_n$ sao cho $G_i:=G[v_1,v_2,\ldots,v_i]$ là đồ thị liên thông với mọi $i$ . Do $G$ là một cây nên mỗi $G_i$ là một cây. Giả sử $G_i$ có $i-1$ cạnh với mọi chỉ số $i<k$ ( $k$ là một số nguyên dương sao cho $k\leq n$ ). Vì $G_k$ là liên thông nên với mỗi $i<k$ , có đường đi trong $G_k$ nối $v_i$ và $v_k$ . Trong tất cả các đường đi như thế, xét đường đi ngắn nhất và giả sử nó nối $v_1$ và $v_k$ . Đường đi này phải có độ dài bằng $1$ , hay $v_k$ và $v_1$ kề nhau trong $G$ . Vì $G$ không có chu trình nên trong $G_{k-1}$ , chỉ có đúng một đỉnh kề với $v_k$ , suy ra $G_k$ có $k-2+1=k-1$ cạnh. Theo nguyên lý quy nạp toán học, $G=G_n$ có $n-1$ cạnh.

Ngược lại, giả sử $G$ là một đồ thị liên thông trên $n$ đỉnh và có $n-1$ cạnh. Gọi $T$ là một đồ thị con bao trùm liên thông cực tiểu của $G$ . Do tính cực tiểu, khi bỏ mỗi cạnh ra khỏi $T$ thì đồ thị thu được không liên thông, suy ra theo định lý 1 thì $T$ là một cây. Cây này có số cạnh bằng $n-1$ theo phần đầu của chứng minh, do đó $T=G$ . $\Box$

Trong một số vấn đề, việc xét một cây với gốc sẽ rất thuận tiện. Giả sử có một cây $T$ và một đỉnh cố định $r$ , gọi là gốc của cây. Với hai đỉnh $x$ và $y$ của $T$ , có đúng một đường đi nối $x$ và $y$ , ta ký hiệu nó là $xTy$ . Với $a,b\in T$ , ta viết $a\leq_T b$ (hoặc $a\leq b$ khi không sợ nhầm lẫn) nếu $a\in rTb$ . Ta thấy $\leq_T$ là một quan hệ thứ tự bộ phận trên $T$ , gọi là thứ tự cây. Khi $a<b$ ta nói $b$ nằm trên $a$ , hay $a$ nằm dưới $b$ . Theo quan hệ thứ tự này thì $r$ là phần tử nhỏ nhất của $T$ , mỗi lá là phần tử cực đại. Hai đầu mút của mỗi cạnh của $T$ là so sánh được.

Ví dụ 2. Cho số nguyên $n$ lớn hơn $1$ và một cây trên $n$ đỉnh. Các đỉnh của cây được viết các số thực $x_1$ , $x_2$ , $\ldots$ , $x_n$ . Mỗi cạnh của cây được viết tích của hai số được viết trên các đầu mút của cạnh, gọi $S$ là tổng tất cả các số này. Chứng minh rằng

$\displaystyle\sqrt{n-1}\left(x_1^2+x_2^2+\dots+x_n^2\right)\geq 2S.$

Lời giải. Giả sử tập các đỉnh của cây là $V=\{v_1, v_2, \ldots, v_n\}$ sao cho với mỗi $i$ , số được viết trên $v_i$ là $x_i$ . Với hai đỉnh kề nhau $v_i$ và $v_j$ , gọi $P(i,j)$ là tập các đỉnh của cây không nối được đến $v_i$ bởi một đường đi sau khi xóa khỏi cây cạnh $v_iv_j$ . Ta có ngay $1\leq \mid P(i,j)\mid \leq n-1$ mỗi khi $v_i$ và $v_j$ kề nhau.

Nhận xét 1. Nếu $v_i$ và $v_j$ kề nhau thì $\mid P(i,j)\mid +\mid P(j,i)\mid=n$ .

Chứng minh. Gọi $v$ là một đỉnh của cây, và xem nó là gốc. Ta có $v_i$ và $v_j$ là so sánh được theo thứ tự cây. Nếu $v_i<v_j$ thì $v\in P(j,i)$ , nếu $v_j<v_i$ thì $v\in P(i,j)$ , nhưng không thể có cả hai. Như vậy $V$ được phân hoạch thành $P(i,j)$ và $P(j,i)$ , từ đây ta có điều cần chứng minh. $\Box$

Nhận xét 2. Với mỗi $i$ ,

$\displaystyle \sum_{v_j\in N(v_i)}\mid P(i,j)\mid =n-1$ .

Chứng minh. Cố định một chỉ số $i$ . Do mỗi đỉnh đều nối đến $v_i$ bởi một đường đi duy nhất và cây không có chu trình nên các $P(i,j)$ với $v_j\in N(v_i)$ làm thành một phân hoạch của $V\setminus\{v_i\}$ , từ đây ta có điều cần chứng minh. $\Box$

Bây giờ với mỗi cạnh $v_iv_j$ , theo nhận xét 1 ta có

$\displaystyle \mid P(i,j)\mid .\mid P(j,i)\mid=\frac{n^2-(\mid P(i,j)\mid -\mid P(j,i)\mid)^2}{4}\geq n-1,$

suy ra

$\displaystyle\frac{\mid P(i,j)\mid}{\sqrt{n-1}}x_i^2+\frac{\mid P(j,i)\mid}{\sqrt{n-1}}x_j^2\geq 2\sqrt{\frac{\mid P(i,j)\mid .\mid P(j,i)\mid}{n-1}}|x_ix_j|\geq 2x_ix_j.$

Mỗi cạnh cho ta một bất đẳng thức có dạng như trên, cộng theo vế các bất đẳng thức này ta có bất đẳng thức trong đề bài. $\Box$

Tài liệu tham khảo

[1] https://nttuan.org/2009/08/13/graph01/

[2] https://nttuan.org/2023/09/01/graph02/

[3] https://nttuan.org/2024/06/04/graph03/

[4] https://nttuan.org/2024/07/01/connected-graph/

Conditional probability

Bạn đọc nên xem lại hai bài sau

[1] https://nttuan.org/2024/01/24/naive-definition-of-probability/

[2] https://nttuan.org/2024/06/02/probability-space/

—

Nhiều phát biểu về cơ hội có dạng: Nếu 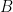$B$ xảy ra thì xác suất để $A$ xảy ra là $p$ . Trong bài này ta sẽ quan tâm đến các phát biểu như vậy.

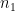Ví dụ 1. Giả sử một lớp học có $n$ học sinh, trong đó có $n_1$ bạn giỏi toán và 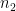$n_2$ bạn nữ. Chọn ngẫu nhiên một học sinh trong lớp. Gọi $A$ là biến cố học sinh được chọn giỏi toán, và 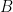$B$ là biến cố học sinh được chọn là nữ. Khi đó theo định nghĩa ngây thơ của xác suất, $\mathbb{P}(A)=n_1/n$ và $\mathbb{P}(B)=n_2/n$ . Bây giờ ta tập trung vào nhóm các bạn học sinh nữ trong lớp. Xác suất để em được chọn trong nhóm này mà giỏi toán bằng $m/n_2$ , ở đây $m$ là số học sinh nữ trong lớp giỏi toán. Nếu kí hiệu $\mathbb{P}(A\mid B)$ là xác suất này, thì

$\displaystyle \mathbb{P}(A\mid B)=\frac{m}{n_2}=\frac{m/n}{n_2/n}=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}.$ $\Box$

Ta có định nghĩa hình thức sau

Định nghĩa 1. Cho một không gian xác suất $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ và hai biến cố $\displaystyle A$ , $\displaystyle B$ với $\displaystyle \mathbb{P}(B)>0$ . Xác suất của $\displaystyle A$ biết $\displaystyle B$ đã xảy ra, cũng được gọi là xác suất của $\displaystyle A$ với điều kiện $\displaystyle B$ , kí hiệu $\displaystyle \mathbb{P}(A\mid B)$ , được định nghĩa bởi

$\displaystyle\mathbb{P}(A\mid B)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}.$

Chú ý rằng $\displaystyle\mathbb{P}(A\mid B)$ là xác suất của $\displaystyle A$ khi biết $\displaystyle B$ xảy ra, nó không phải là xác suất của biến cố $\displaystyle A\mid B$ , không có biến cố $\displaystyle A\mid B$ . Nếu $\displaystyle \mathbb{P}(A)>0$ thì $\displaystyle \mathbb{P}(A\mid A)=1$ .

Ví dụ 2. Xét phép thử ngẫu nhiên: Tung lần lượt hai con xúc xắc cân đối. Biết rằng con xúc xắc đầu hiện $\displaystyle 3$ chấm, xác suất để tổng số chấm lớn hơn $\displaystyle 6$ là bao nhiêu?

Lời giải. Không gian mẫu của phép thử là $\displaystyle \Omega=\{1,2,3,4,5,6\}^2$ . Như quy ước đối với không gian xác suất rời rạc, $\displaystyle \mathcal{F}$ là họ tất cả các tập con của $\displaystyle \Omega$ . Cuối cùng, $\displaystyle \mathbb{P}(A)=\mid A\mid / 36$ với mỗi $\displaystyle A \subset \Omega$ .

Bây giờ gọi $\displaystyle B$ là biến cố con đầu ra $\displaystyle 3$ chấm, và $\displaystyle A$ là biến cố tổng các chấm lớn hơn $\displaystyle 6$ . Khi đó

$\displaystyle B=\{(3, b): 1 \leq b \leq 6\}, \quad A=\{(a, b): a+b>6\},$ $\displaystyle \quad A \cap B=\{(3,4),(3,5),(3,6)\}.$ Suy ra

$\displaystyle \mathbb{P}(A \mid B)=\frac{\mathbb{P}(A \cap B)}{\mathbb{P}(B)}=\frac{|A \cap B|}{|B|}=\frac{3}{6}=\frac{1}{2}.$ $\Box$

Ví dụ 3. Rút ngẫu nhiên hai quân bài từ một bộ bài cho trước, mỗi lần rút một quân và không trả lại. Gọi $\displaystyle A$ là sự kiện quân bài thứ nhất mang chất cơ và $\displaystyle B$ là sự kiện quân bài thứ hai có màu đỏ. Tính $\displaystyle \mathbb{P}(A\mid B)$ và $\displaystyle \mathbb{P}(B\mid A)$ .

Lời giải. Không gian xác suất được xây dựng theo cách tự nhiên. Với không gian xác suất này, $\displaystyle \mathbb{P}(A)=1/4$ , $\displaystyle \mathbb{P}(B)=1/2$ , và $\displaystyle\mathbb{P}(A\cap B)=\frac{25}{204}.$ Từ đây ta thu được

$\displaystyle\mathbb{P}(A\mid B)=\frac{\mathbb{P}(A\cap B)}{\mathbb{P}(B)}=\frac{25}{102}\approx 0,25$

và

$\displaystyle\mathbb{P}(B\mid A)=\frac{\mathbb{P}(B\cap A)}{\mathbb{P}(A)}=\frac{25}{51}\approx 0,49.$ $\Box$

Từ định nghĩa của xác suất có điều kiện ta có

Định lý 1 (Công thức Bayes). Cho một không gian xác suất $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ và hai biến cố $\displaystyle A$ , $\displaystyle B$ với $\displaystyle \mathbb{P}(A)\mathbb{P}(B)>0$ . Khi đó

$\displaystyle\mathbb{P}(A\mid B)=\frac{\mathbb{P}(B\mid A)\mathbb{P}(A)}{\mathbb{P}(B)}.$

Định lý 2 (Công thức xác suất toàn phần). Cho một không gian xác suất $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ . Giả sử $\displaystyle A_1$ , $\displaystyle A_2$ , $\displaystyle \ldots$ , $\displaystyle A_n$ là một phân hoạch của $\displaystyle\Omega$ sao cho $\displaystyle \mathbb{P}(A_i)>0$ với mọi $\displaystyle i$ . Khi đó với mỗi biến cố $\displaystyle B$ ,

$\displaystyle\mathbb{P}(B)=\sum_{i=1}^n\mathbb{P}(B\mid A_i)\mathbb{P}(A_i).$

Công thức xác suất toàn phần cho một liên hệ giữa xác suất có điều kiện và xác suất không điều kiện. Để tính một xác suất, ta có thể dùng công thức này để chia bài toán thành các bài toán đơn giản hơn, và nó thường được sử dụng cùng với công thức Bayes.

Ví dụ 4. Có hai chiếc hộp, $\displaystyle \alpha$ và $\displaystyle \beta$ , đựng các viên bi xanh và đỏ. Hộp $\displaystyle \alpha$ chứa hai viên bi đỏ và ba viên bi xanh, hộp $\displaystyle \beta$ chứa ba viên bi đỏ và bốn viên bi xanh. Một viên bi được lấy ngẫu nhiên từ hộp $\displaystyle \alpha$ và bỏ vào hộp $\displaystyle \beta$ . Sau đó, lấy ngẫu nhiên một viên bi trong hộp $\displaystyle \beta$ và kiểm tra màu của nó. Xác suất để nó có màu xanh là bao nhiêu?

Lời giải. Không gian xác suất được mô tả theo cách tự nhiên. Gọi $\displaystyle A$ là biến cố viên bi lấy sau mang màu xanh, và $\displaystyle B$ là biến cố viên bi lấy trước mang màu xanh. Tính toán đơn giản ta được $\displaystyle \mathbb{P}(B)=3/5>0$ và $\displaystyle\mathbb{P}(\overline{B})=2/5>0$ , do đó theo công thức xác suất toàn phần, ta có

$\displaystyle\mathbb{P}(A)=\mathbb{P}(A\mid B)\mathbb{P}(B)+\mathbb{P}(A\mid \overline{B})\mathbb{P}(\overline{B}).$

Mà ta lại có $\displaystyle \mathbb{P}(A\mid B)=5/8$ và $\displaystyle \mathbb{P}(A\mid \overline{B})=1/2$ , suy ra $\displaystyle \mathbb{P}(A)=23/40= 0,575.$ $\Box$

Ví dụ 5. Có hai nhà máy sản xuất cốc, nhà máy I và nhà máy II. Biết rằng $\displaystyle 20\%$ số cốc từ nhà máy I và $\displaystyle 5\%$ từ nhà máy II bị lỗi. Mỗi tuần, I sản xuất số lượng cốc gấp đôi II. Xác suất để một chiếc cốc được chọn ngẫu nhiên trong một tuần sản xuất đạt yêu cầu là bao nhiêu? Nếu chiếc cốc được chọn bị lỗi thì khả năng nó được sản xuất bởi I là bao nhiêu?

Lời giải. Gọi $\displaystyle A$ là biến cố mà chiếc cốc được chọn là đạt yêu cầu, và gọi $\displaystyle B$ là biến cố nó được sản xuất tại $\displaystyle I$ . Khi đó

$\displaystyle\mathbb{P}(A)=\mathbb{P}(A\mid B)\mathbb{P}(B)+\mathbb{P}(A\mid \overline{B})\mathbb{P}(\overline{B})$

$=\frac{4}{5}\cdot\frac{2}{3}+\frac{19}{20}\cdot\frac{1}{3}=\frac{51}{60}\approx 0,85.$

Nếu chiếc cốc được chọn bị lỗi thì khả năng nó được sản xuất bởi I, theo công thức Bayes, là

$\displaystyle \mathbb{P}(B\mid \overline{A})=\frac{\mathbb{P}(\overline{A}\mid B)\mathbb{P}(B)}{\mathbb{P}(\overline{A})}=\frac{\frac{1}{5}\cdot \frac{2}{3}}{1-\frac{51}{60}}=\frac{8}{9}\approx 0,889.$ $\Box$

Ví dụ 6. Có một đồng xu công bằng và một đồng xu không công bằng với xác suất hiện mặt sấp khi tung là $\displaystyle 3/4$ . Chọn ngẫu nhiên một trong hai đồng xu và tung nó ba lần. Nó hiện mặt sấp cả ba lần. Tính xác suất để đồng xu được chọn là đồng xu công bằng.

Lời giải. Gọi $\displaystyle A$ là biến cố đồng xu được chọn đều hiện mặt sấp khi tung ba lần, và $\displaystyle B$ là biến cố đồng xu được chọn là đồng xu công bằng. Theo công thức Bayes và công thức xác suất toàn phần, ta có

$\displaystyle \mathbb{P}(B \mid A)=\frac{\mathbb{P}(A \mid B) \mathbb{P}(B)}{\mathbb{P}(A)}=\frac{\mathbb{P}(A \mid B) \mathbb{P}(B)}{\mathbb{P}(A \mid B) \mathbb{P}(B)+\mathbb{P}\left(A \mid \overline{B}\right) \mathbb{P}\left(\overline{B}\right)}$

$=\frac{(1 / 2)^3 \cdot 1 / 2}{(1 / 2)^3 \cdot 1 / 2+(3 / 4)^3 \cdot 1 / 2}\approx 0.23$ . $\Box$

Ví dụ 7. Xét một trò chơi trong đó một người chơi phải chọn một trong ba cánh cửa. Một trong ba cánh cửa giấu một giải thưởng có giá trị là một chiếc ô tô mới, trong khi mỗi một trong hai cánh cửa còn lại giấu một chiếc bút chì. Sau khi người chơi lựa chọn, người dẫn chương trình (biết xe ở đâu) sẽ mở một trong hai cánh cửa mà người chơi không chọn và cho biết phía sau cánh cửa đó có một cái bút chì. Vào thời điểm này, người chơi phải lựa chọn giữa hai cánh cửa còn lại. Người chơi nên giữ nguyên lựa chọn hay thay đổi?

Lời giải. Bởi vì còn hai cách cửa, một chứa ô tô và cánh còn lại chứa bút chì, nên nhiều người cho rằng chọn lại hay giữ nguyên thì khả năng là như nhau. Đây là câu trả lời sai.

Gọi $\displaystyle A_i$ là biến cố giải thưởng ô tô nằm sau cánh cửa $\displaystyle i$ . Giả sử người chơi đã chọn cánh cửa $\displaystyle 1$ . Gọi $\displaystyle B$ là sự kiện người dẫn chương trình mở ra cánh cửa số $\displaystyle 2$ có giải thưởng là cái bút chì. Theo định nghĩa của xác suất có điều kiện và công thức xác suất toàn phần,

$\displaystyle \mathbb{P}\left(A_1 \mid B\right)=\frac{\mathbb{P}\left(A_1 \cap B\right)}{\mathbb{P}(B)}=\frac{\mathbb{P}\left(B \mid A_1\right)\mathbb{P}\left(A_1\right)}{\mathbb{P}\left(B \mid A_1\right) \mathbb{P}\left(A_1\right)+\mathbb{P}\left(B \mid A_2\right) \mathbb{P}\left(A_2\right)+\mathbb{P}\left(B \mid A_3\right) \mathbb{P}\left(A_3\right)}.$

Bây giờ lập luận đơn giản cho ta $\displaystyle\mathbb{P}(A_i)=1/3$ với mọi $\displaystyle i$ , $\displaystyle \mathbb{P}\left(B \mid A_1\right)=1 / 2$ , $\displaystyle P\left(B \mid A_2\right)=0$ , và $\displaystyle \mathbb{P}\left(B \mid A_3\right)=1$ . Suy ra $\displaystyle \mathbb{P}\left(A_1 \mid B\right)=1/3\approx 0,333.$ Như vậy người chơi nên thay đổi lựa chọn của mình. $\Box$

Từ đầu cho đến thời điểm hiện tại ta đã thấy nhiều ví dụ mà $\displaystyle \mathbb{P}(A\mid B)\not=\mathbb{P}(B)$ , nghĩa là khi ta bổ sung thông tin $\displaystyle B$ thì khả năng xảy ra $\displaystyle A$ thay đổi. Nếu khi bổ sung $\displaystyle B$ mà khả năng xảy ra $\displaystyle A$ không thay đổi ta nói $\displaystyle A$ và $\displaystyle B$ là độc lập.

Định nghĩa 2. Cho một không gian xác suất $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ . Một họ các biến cố $\displaystyle \{A_i\}_{i\in I}$ được gọi là độc lập nếu với mỗi tập con hữu hạn $\displaystyle J$ của $\displaystyle I$ ,

$\displaystyle\mathbb{P}\left(\bigcap_{j\in J}A_j\right)=\prod_{j\in J}\mathbb{P}(A_j).$

Từ định nghĩa này ta thấy nếu $\displaystyle A$ và $\displaystyle B$ là hai sự kiện độc lập với $\displaystyle \mathbb{P}(A)\mathbb{P}(B)>0$ thì $\displaystyle \mathbb{P}(A\mid B)=\mathbb{P}(A)$ và $\displaystyle \mathbb{P}(B\mid A)=\mathbb{P}(B)$ .