Chessboard comeback

Trưa nay tôi được hỏi câu V trong đề thi tuyển sinh vào lớp 10 Chuyên toán năm học 2024-2025 của Hà Nội. Trong bài này tôi sẽ phát biểu bài toán tổng quát và giới thiệu một lời giải của bài toán đó.

Bài toán. Cho một số nguyên $n$ lớn hơn $1$ và một bảng ô vuông cỡ $n\times n$ . Ban đầu một số ô vuông của bảng được tô màu đỏ. Sau đó mỗi giây, các ô vuông có chung cạnh với ít nhất hai ô đỏ sẽ được tô đỏ. Hỏi ban đầu cần tô ít nhất bao nhiêu ô vuông để sau một thời gian, tất cả các ô của bảng đều được tô đỏ?

Lời giải. Cần tô màu ít nhất $n$ ô để sau một thời gian, tất cả các ô của bảng đều được tô đỏ.

Mỗi ô vuông con được xem là có cạnh $1$ . Gọi $k$ là số ô được tô đỏ ban đầu, và ở mỗi thời điểm gọi $S$ là tổng chu vi của các vùng được tô đỏ. Ta thấy ban đầu $S\leq 4k$ và nếu tất cả các ô của bảng mang màu đỏ thì $S=4n$ . Để ý rằng sau mỗi giây $S$ không tăng. Vì thế, nếu sau một thời gian các ô đều mang màu đỏ thì $4k\geq 4n$ , suy ra $k\geq n$ .

Bây giờ nếu lúc đầu tô $n$ ô dọc theo một đường chéo chính của bảng thì sau một thời gian, tất cả các ô của bảng đều được tô đỏ. $\Box$

The degree of a vertex

Bài này là phần tiếp theo của bài https://nttuan.org/2023/09/01/graph02/

Cho đồ thị $\displaystyle G=(V,E).$ Bậc của một đỉnh $\displaystyle v\in G,$ ký hiệu $\displaystyle \deg_G(v)$ hoặc $\displaystyle \deg (v),$ là số đỉnh của $\displaystyle G$ kề với $\displaystyle v.$ Đỉnh có bậc bằng $\displaystyle 0$ được gọi là đỉnh cô lập. Đỉnh có bậc bằng $1$ được gọi là lá. Nếu mọi đỉnh của $\displaystyle G$ đều có bậc $\displaystyle k$ thì ta nói $\displaystyle G$ là $\displaystyle k-$ đều.

Định lý 1. Trong mỗi đồ thị có cấp lớn hơn $\displaystyle 1$ , tồn tại ít nhất hai đỉnh có cùng bậc.

Chứng minh. Gọi $\displaystyle n$ là cấp của đồ thị. Bậc của mỗi đỉnh của đồ thị là một số tự nhiên bé hơn $\displaystyle n$ . Vì vậy, nếu các đỉnh của đồ thị có bậc đôi một khác nhau thì có đỉnh cô lập và có đỉnh kề với mọi đỉnh khác, vô lý. $\Box$

Định lý 2. Với mỗi đồ thị $\displaystyle G=(V,E),$ ta có

$\displaystyle \displaystyle \sum_{v\in V}\deg (v)=2\mid E\mid.$

Chứng minh. Khi ta cộng tất cả bậc của các đỉnh, ta đã đếm mỗi cạnh đúng hai lần, một cho mỗi đầu mút của nó. $\Box$

Hệ quả. Số đỉnh bậc lẻ trong một đồ thị là số chẵn.

Ví dụ 1. Có đồ thị với dãy bậc của đỉnh như sau hay không?

(a) $\displaystyle 3,2,2,2.$

(b) $\displaystyle 3,3,2,2.$

Hướng dẫn. Ý đầu là không vì tổng bậc phải chẵn, ý thứ hai là có. Ý thứ ba là không, vì nếu có thì khi xét hai đỉnh bậc $\displaystyle 4,$ có ít nhất $\displaystyle 6$ cạnh đến các đỉnh bậc $\displaystyle 1,$ vô lý. $\Box$

Vào năm 1960, Paul Erdos và Tibor Gallai đã tìm được kết quả sau:

Định lý 3 (Erdos-Gallai). Dãy số nguyên không âm $\displaystyle d_1\geq d_2\geq\ldots \geq d_n$ là dãy bậc của một đồ thị trên $\displaystyle n$ đỉnh khi và chỉ khi $\displaystyle \sum d_i$ chẵn và

$\displaystyle \sum_{i=1}^kd_i\leq k(k-1)+\sum_{i=k+1}^n\min\{d_i,k\},\quad \forall k=\overline{1,n}.$

Ví dụ 2. Cho một tập hợp $\displaystyle S$ gồm $\displaystyle 100$ điểm trong mặt phẳng sao cho khoảng cách giữa hai điểm bất kỳ trong $\displaystyle S$ không bé hơn $\displaystyle 1.$ Chứng minh rằng có không nhiều hơn $\displaystyle 300$ cặp điểm (không kể thứ tự) mà khoảng cách giữa hai điểm trong mỗi cặp bằng $\displaystyle 1.$

Hướng dẫn. Xét đồ thị $\displaystyle G$ trên $\displaystyle S$ được xác định như sau: Tập con $\displaystyle \{A,B\}$ của $\displaystyle S$ là một cạnh của $\displaystyle G$ khi và chỉ khi $\displaystyle AB=1.$ Vì $\displaystyle \deg (v)\leq 6$ với mọi $\displaystyle v\in S$ , nên $\displaystyle \mid E(G)\mid \leq 1/2\times 6\times 100=300$ . $\Box$

Ví dụ 3. Cho một lớp học có số học sinh là số chẵn. Chứng minh rằng tồn tại hai học sinh trong lớp có số người quen chung trong lớp là số chẵn.

Lời giải. Xét đồ thị $\displaystyle G$ trên tập hợp $\displaystyle V$ các học sinh trong lớp được xác định như sau: với hai đỉnh $\displaystyle a$ và $\displaystyle b$ của $\displaystyle G,$ có một cạnh nối $\displaystyle a$ và $\displaystyle b$ khi $\displaystyle a$ và $\displaystyle b$ quen nhau. Giả sử ngược lại rằng với mỗi $\displaystyle a$ và $\displaystyle b$ phân biệt thuộc $\displaystyle V,$ $\displaystyle \mid N(a)\cap N(b)\mid$ là số lẻ. Nói riêng, mỗi hai đỉnh có ít nhất một láng giềng chung.

Nhận xét. Mọi đỉnh của $\displaystyle G$ đều có bậc chẵn.

Chứng minh. Xét một đỉnh $\displaystyle x$ bất kỳ và xem $\displaystyle N(x)$ như đồ thị con cảm sinh của $\displaystyle G.$ Ta thấy $\displaystyle \sum_{y\in N(x)}\deg_{N(x)}(y)$ là số chẵn và mỗi số hạng là lẻ, suy ra $\mid N(x)\mid$ là số chẵn. $\Box$

Bây giờ cố định một đỉnh $\displaystyle x$ bất kỳ của $\displaystyle G.$ Đặt $\displaystyle X=V\setminus (N(x)\cup \{x\}).$ Khi đó $\displaystyle X$ có số phần tử lẻ. Ta quan tâm đến số $\displaystyle \alpha$ các cạnh có một đầu mút thuộc $\displaystyle X$ đầu mút kia thuộc $\displaystyle N(x)$ theo hai cách. Nếu chọn đầu mút thuộc $\displaystyle X$ trước thì ta thấy $\displaystyle \alpha$ là số lẻ, trong khi nếu chọn đầu mút thuộc $\displaystyle N(x)$ trước thì ta thấy $\displaystyle \alpha$ là số chẵn (theo nhận xét), vô lý. $\Box$

Continue reading →

Probability space

Các bạn đọc lại bài https://nttuan.org/2024/01/24/naive-definition-of-probability/ để theo dõi bài cho dễ dàng.

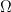Một họ $\mathcal{G}$ các tập con của một tập hợp $\Omega$ được gọi là một đại số các tập con của 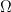$\Omega$ nếu nó có ba tính chất sau:

(1) $\Omega\in\mathcal{G}$ .

(2) Nếu $C\in \mathcal{G}$ thì $\Omega\setminus C\in\mathcal{G}$ .

(3) Nếu $C_1,C_2,\ldots,C_n\in\mathcal{G}$ thì $\displaystyle \bigcup_{i=1}^nC_i\in\mathcal{G}$ .

Ví dụ 1. Với tập hợp $\displaystyle \Omega$ , ta có họ $\displaystyle \mathcal{G}=\{\emptyset,\Omega\}$ là một đại số các tập con của $\displaystyle \Omega$ . $\Box$

Bổ đề 1. Cho $\displaystyle \mathcal{G}$ là một đại số các tập con của $\displaystyle \Omega$ . Khi đó

(1) $\displaystyle \emptyset\in\mathcal{G}$ .

(2) Nếu $\displaystyle C_1,C_2,\ldots,C_n\in\mathcal{G}$ thì $\displaystyle \bigcap_{i=1}^nC_i\in\mathcal{G}$ .

(3) Nếu $\displaystyle C_1,C_2\in\mathcal{G}$ thì $C_1\setminus C_2\in\mathcal{G}$ .

Chứng minh. Vì $\displaystyle \Omega\in\mathcal{G}$ nên $\displaystyle \emptyset=\Omega\setminus\Omega$ cũng thuộc $\displaystyle \mathcal{G}$ . Nếu $\displaystyle C_1$ , $\displaystyle C_2$ , $\displaystyle \ldots$ , $\displaystyle C_n\in\mathcal{G}$ thì

$\displaystyle \Omega\setminus \bigcap_{i=1}^nC_i=\bigcup_{i=1}^n(\Omega\setminus C_i)\in\mathcal{G},$

suy ra $\displaystyle \bigcap_{i=1}^nC_i\in\mathcal{G}$ . Cuối cùng, nếu $\displaystyle C_1$ , $\displaystyle C_2\in\mathcal{G}$ thì $\displaystyle C_1\setminus C_2=\Omega\setminus ((\Omega\setminus C_1)\cup C_2)\in\mathcal{G}.$ $\Box$

Định nghĩa 1. Một họ $\displaystyle \mathcal{G}$ các tập con của một tập hợp $\displaystyle \Omega$ được gọi là một $\displaystyle \sigma-$ đại số các tập con của $\displaystyle \Omega$ nếu nó có ba tính chất sau:

(1) $\displaystyle \Omega\in\mathcal{G}$ .

(2) Nếu $\displaystyle C\in \mathcal{G}$ thì $\displaystyle \Omega\setminus C\in\mathcal{G}$ .

(3) Nếu $\displaystyle C_1,C_2,\ldots\in\mathcal{G}$ thì $\displaystyle \bigcup_{i=1}^{\infty}C_i\in\mathcal{G}$ .

Lúc này ta gọi $\displaystyle \Omega$ là không gian mẫu và các phần tử của $\displaystyle \mathcal{G}$ là các biến cố, hay sự kiện.

Mỗi $\displaystyle \sigma-$ đại số là một đại số, ngược lại không đúng.

Ví dụ 2. $\displaystyle \sigma-$ đại số nhỏ nhất các tập con của $\displaystyle \Omega$ là $\displaystyle \{\emptyset,\Omega\}$ . $\Box$

Ví dụ 3. Nếu $\displaystyle A$ là một tập con của $\displaystyle \Omega$ thì $\displaystyle \{\emptyset,\Omega,A,\overline{A}\}$ là một $\displaystyle \sigma-$ đại số các tập con của $\displaystyle \Omega$ . $\Box$

Ví dụ 4. Họ tất cả các tập con của $\displaystyle \Omega$ là $\displaystyle \sigma-$ đại số lớn nhất các tập con của $\displaystyle \Omega$ . $\Box$

Định nghĩa 2. Một không gian đo được là một cặp $\displaystyle (\Omega,\mathcal{F})$ , trong đó $\displaystyle \Omega$ là một tập hợp và $\displaystyle \mathcal F$ là một $\displaystyle \sigma-$ đại số các tập con của $\displaystyle \Omega$ . Khi $\displaystyle \Omega$ là hữu hạn hoặc đếm được thì không gian đo được $\displaystyle (\Omega,\mathcal{F})$ được gọi là rời rạc.

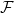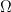Mỗi khi xét không gian đo được rời rạc $(\Omega,\mathcal{F})$ , ta chỉ xét $\mathcal F$ là $\sigma-$ đại số tất cả các tập con của $\Omega$ .

Định nghĩa 3. Cho một không gian đo được $\displaystyle (\Omega,\mathcal{F})$ . Độ đo xác suất $\displaystyle \mathbb{P}$ trên $\displaystyle (\Omega,\mathcal{F})$ là một hàm $\displaystyle \mathbb{P}:\mathcal{F}\to [0;1]$ thỏa mãn đồng thời hai điều sau:

(1) $\displaystyle \mathbb{P}(\emptyset)=0$ và $\mathbb{P}(\Omega)=1$ .

(2) Nếu $\displaystyle A_1,A_2,\ldots$ là một dãy các phần tử đôi một rời nhau của $\displaystyle \mathcal F$ thì $\displaystyle \mathbb{P}\left(\bigcup_{i=1}^{\infty}A_i\right)=\sum_{i=1}^{\infty}\mathbb{P}(A_i).$

Lúc này thì bộ ba $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ được gọi là không gian xác suất. Với mỗi sự kiện $\displaystyle A$ , ta gọi $\displaystyle \mathbb{P}(A)$ là xác suất của $\displaystyle A$ .

Với không gian xác suất $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ và biến cố $\displaystyle A$ , ta gọi $\displaystyle A$ là biến cố rỗng nếu $\displaystyle \mathbb{P}(A)=0$ và là biến cố chắc chắn nếu $\displaystyle \mathbb{P}(A)=1$ . Ta có thể xác định một không gian xác suất tương ứng với mỗi phép thử. Khi đó các bài toán liên quan đến phép thử sẽ chuyển về các bài toán trong không gian xác suất tương ứng.

Ví dụ 5. Một đồng xu, có thể không cân, được tung lên một lần. Với phép thử này ta xác định không gian xác suất $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ như sau: Không gian mẫu $\displaystyle \Omega=\{0;1\}$ (như trong bài trước, sấp được ghi là $\displaystyle 1$ và ngửa được ghi là $\displaystyle 0$ ), $\displaystyle \mathcal{F}$ là họ tất cả các tập con của $\displaystyle \Omega$ , và độ đo xác suất $\displaystyle \mathbb{P}:\mathcal{F}\to [0;1]$ được định nghĩa bởi

$\displaystyle\mathbb{P}(\emptyset)=0,\,\mathbb{P}(\Omega)=1,\,\mathbb{P}(\{1\})=p,\,\mathbb{P}(\{0\})=1-p.$

Ở đây $\displaystyle p$ là một số thực thuộc đoạn $\displaystyle [0;1]$ . Đồng xu này là cân đối nếu $\displaystyle p=1/2$ . $\Box$

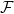Ví dụ 6. Một con xúc xắc được tung một lần. Với phép thử này ta xác định không gian xác suất $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ như sau: Không gian mẫu $\displaystyle \Omega=[6]$ , $\mathcal{F}$ là họ tất cả các tập con của $\displaystyle \Omega$ , và độ đo xác suất $\displaystyle \mathbb{P}:\mathcal{F}\to [0;1]$ được định nghĩa bởi

$\displaystyle \mathbb{P}(A)=\sum_{i\in A}p_i, \quad \forall A\subset \Omega.$

Ở đây $\displaystyle p_1,p_1,\ldots,p_6$ là các số thực không âm có tổng bằng $\displaystyle 1$ . Xác suất để xuất hiện mặt có $\displaystyle i$ chấm là $\displaystyle p_i$ . Con xúc xắc này là cân đối nếu các $\displaystyle p_i$ đều bằng $\displaystyle 1/6$ . Khi đó $\displaystyle \mathbb{P}(A)=\frac{\mid A\mid }{6}, \quad \forall A\subset \Omega,$ bằng xác suất xảy ra $\displaystyle A$ theo định nghĩa ngây thơ (cổ điển) của xác suất. $\Box$

Sau đây là một số tính chất của độ đo xác suất.

Bổ đề 2. Cho một không gian xác suất $\displaystyle (\Omega,\mathcal{F},\mathbb{P})$ . Khi đó

(1) Với mỗi biến cố $A$ , ta có $\displaystyle \mathbb{P}(\overline{A})=1-\mathbb{P}({A})$ .

(2) Nếu $\displaystyle A$ và $\displaystyle B$ là các biến cố thỏa mãn $\displaystyle A\subset B$ thì $\displaystyle \mathbb{P}({B})=\mathbb{P}({A})+\mathbb{P}({B\setminus A})\geq \mathbb{P}({A}).$

(3) Nếu $\displaystyle A_1,A_2,\ldots,A_n$ là $\displaystyle n>1$ biến cố thì

$\displaystyle \mathbb{P}\left(\bigcup_{i=1}^nA_i\right)=\sum_{i=1}^n\mathbb{P}({A_i})-\sum_{i<j}\mathbb{P}({A_i\cap A_j})+\sum_{i<j<k}\mathbb{P}({A_i\cap A_j\cap A_k})$ $\displaystyle -\ldots +(-1)^{n+1}\mathbb{P}(A_1\cap A_2\cap \ldots \cap A_n).$

Chứng minh. Xét một biến cố $\displaystyle A$ . Vì $\displaystyle\Omega=A\cup\overline{A}$ và $\displaystyle A\cap\overline{A}=\emptyset$ nên

$\displaystyle 1=\mathbb{P}(\Omega)=\mathbb{P}(A\cup\overline{A})=\mathbb{P}({A})+\mathbb{P}\overline{A}),$

suy ra $\displaystyle \mathbb{P}(\overline{A})=1-\mathbb{P}({A})$ . Bây giờ xét hai biến cố $\displaystyle A$ và $\displaystyle B$ với $\displaystyle A\subset B$ . Vì biến cố $\displaystyle B$ là hợp của hai biến cố rời nhau $\displaystyle A$ và $\displaystyle B\setminus A$ nên

$\displaystyle\mathbb{P}({B})=\mathbb{P}({A})+\mathbb{P}({B\setminus A})\geq \mathbb{P}({A}).$

Ta sẽ chứng minh khẳng định cuối cùng bằng quy nạp theo 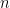$\displaystyle n$ . Xét hai biến cố $\displaystyle A$ và $\displaystyle B$ . Biến cố $\displaystyle A\cup B$ là hợp của hai biến cố rời nhau $\displaystyle A$ và $\displaystyle B\setminus A$ nên

$\displaystyle\mathbb{P}(A\cup {B}) =\mathbb{P}({A})+\mathbb{P}({B\setminus A})= \mathbb{P}({A})+\mathbb{P}({B\setminus (A\cap B)})=\mathbb{P}({A})+\mathbb{P}({B})-\mathbb{P}(A\cap B),$

suy ra khẳng định đúng với $\displaystyle n=2$ . Bây giờ giả sử khẳng định đúng với số nguyên dương $\displaystyle n= k\, (k>1)$ . Xét $\displaystyle k+1$ biến cố $\displaystyle A_1$ , $\displaystyle A_2,\ldots,$ $\displaystyle A_{k+1}$ . Vì khẳng định đúng với $\displaystyle n=2$ nên

$\displaystyle \mathbb{P}\left(\bigcup_{i=1}^{k+1}A_i\right)=\mathbb{P}\left(\left(\bigcup_{i=1}^{k}A_i\right)\bigcup A_{k+1}\right)$

$\displaystyle =\mathbb{P}\left(\bigcup_{i=1}^{k}A_i\right)+\mathbb{P}\left(A_{k+1}\right)-\mathbb{P}\left(\left(\bigcup_{i=1}^{k}A_i\right)\bigcap A_{k+1}\right)$

$\displaystyle =\mathbb{P}\left(\bigcup_{i=1}^{k}A_i\right)+\mathbb{P}\left(A_{k+1}\right)-\mathbb{P}\left(\bigcup_{i=1}^{k}\left(A_i\bigcap A_{k+1}\right)\right).$

Đến đây dùng giả thiết quy nạp ta thấy khẳng định đúng với $\displaystyle n=k+1$ . Theo nguyên lý quy nạp toán học, khẳng định đúng với mỗi số nguyên $\displaystyle n>1$ . $\Box$