Day: September 1, 2023

Graph theory: Basic definitions


Đây là bài thứ hai của tôi về lý thuyết đồ thị. Các bạn có thể xem bài trước ở

[1] https://nttuan.org/2023/08/13/graph01/

Với mỗi tập hợp X, ký hiệu [X]^2 là tập gồm tất cả các tập con có 2 phần tử của X.

Định nghĩa 1. Một đồ thị là một cặp G=(V,E) các tập hợp sao cho E\subset [V]^2.

Như vậy, các phần tử của E là các tập con có 2 phần tử của V. Các phần tử của V được gọi là các đỉnh của đồ thị G, các phần tử của E được gọi là các cạnh của G. Đồ thị có tập các đỉnh V được gọi là đồ thị trên V. Cách thông thường để vẽ một đồ thị là mỗi đỉnh biểu thị bởi một dấu chấm và nối hai trong các dấu chấm này bởi một đường cong nếu hai đỉnh tương ứng tạo thành một cạnh.

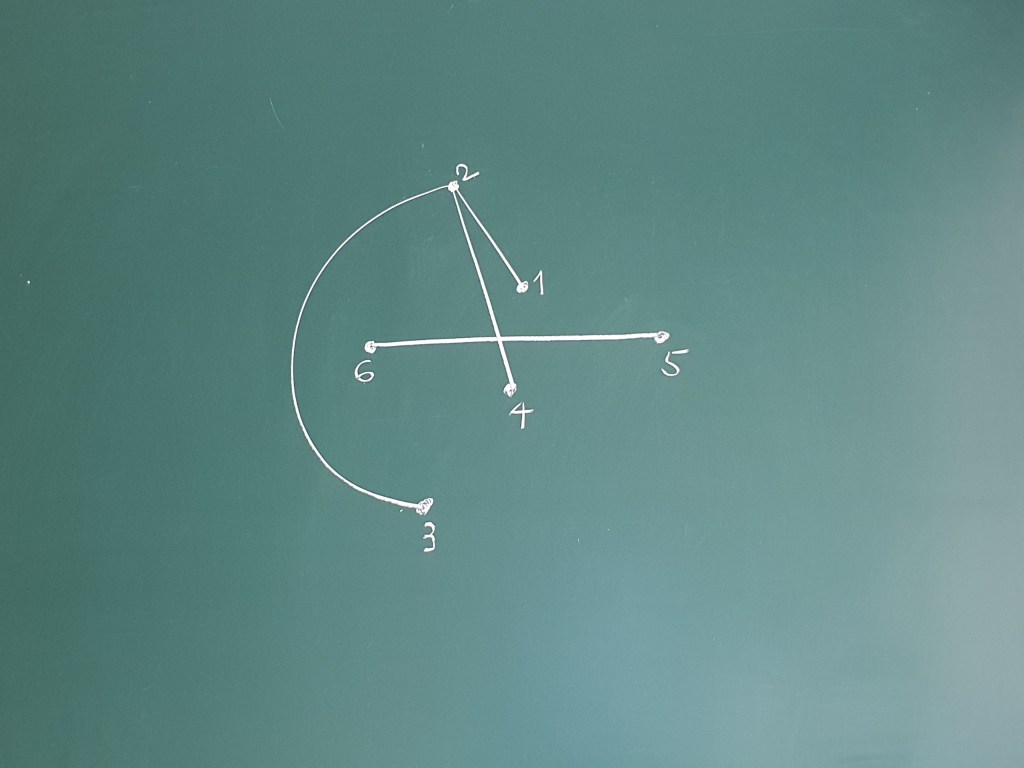
Trong hình trên ta có một đồ thị trên V=\{1,2,\ldots,6\} với tập cạnh E=\{\{1;2\},\{2;3\},\{6;5\},\{2;4\}\}. Khi vẽ một đồ thị ta không quan tâm các đỉnh hay cạnh được vẽ thế nào, điều quan trọng duy nhất ở đây là hai đỉnh nào được nối với nhau. Tập các đỉnh của một đồ thị G được ký hiệu bởi V(G), trong khi tập cạnh của nó được ký hiệu bởi E(G). Ta thường không phân biệt đồ thị và tập cạnh hoặc tập đỉnh của nó. Chẳng hạn, ta có thể nói đỉnh v thuộc G (thay vì v\in V(G)), một cạnh e của G,…

Số đỉnh của G được gọi là cấp của nó, ký hiệu bởi \mid G\mid. Một đồ thị G được gọi là hữu hạn nếu V(G) và E(G) là hai tập hữu hạn, vô hạn nếu V(G) hoặc E(G) là một tập vô hạn. Trong bài giảng này ta chỉ xét các đồ thị hữu hạn. Khi \mid G\mid =0 ta gọi G là đồ thị rỗng, ký hiệu \emptyset. Nếu cấp của G bằng n thì ta cũng nói G là đồ thị trên n đỉnh.

Định nghĩa 2. Cho một đồ thị G. Đỉnh v của G được gọi là đầu mút của một cạnh e của G nếu v\in e. Nếu hai đầu mút của một cạnh e là x và y thì ta nói e nối x và y, hoặc e kề với hai đỉnh x và y.

Một cạnh \{x;y\} thường được viết là xy hoặc yx.

Định nghĩa 3. Cho một đồ thị G. Hai đỉnh x và y của G được gọi là kề nhau nếu \{x;y\} là một cạnh của G. Trong trường hợp đó ta nói x và y là láng giềng của nhau.

Với mỗi đỉnh x, tập gồm tất cả các đỉnh kề với x được ký hiệu là N(x) hoặc N_G(x). Hai cạnh phân biệt e và f của G được gọi là kề nhau nếu chúng có chung một đầu mút. Nếu tất cả các đỉnh của G là đôi một kề nhau ta nói G là một đồ thị đầy đủ. Một đồ thị đầy đủ trên n đỉnh được ký hiệu bởi K_n. K_3 được gọi là tam giác. Một cặp các đỉnh hay cạnh được gọi là độc lập nếu chúng không kề nhau.

Định nghĩa 4. Cho hai đồ thị G=(V,E) và G^{\prime}=(V^{\prime},E^{\prime}). Một ánh xạ \varphi: V\to V^{\prime} được gọi đồng cấu từ G đến G^{\prime} nếu nó bảo toàn quan hệ kề giữa các đỉnh, nghĩa là \varphi (x) và \varphi (y) kề nhau mỗi khi x và y kề nhau. Nếu đồng cấu \varphi từ G đến G^{\prime} là một song ánh và \varphi^{-1} cũng là một đồng cấu, thì ta nói \varphi là một đẳng cấu hoặc G và G^{\prime} là đẳng cấu.

Ta không phân biệt các đồ thị đẳng cấu, vì thế ta thường viết G=G^{\prime} để chỉ G và G^{\prime} đẳng cấu. Trong một số trường hợp ta cũng nói G^{\prime} là một bản sao của G.

Continue reading “Graph theory: Basic definitions” →