IMO2011/6: Miquel circles and Steiner line

Sau khi giải xong bài IMO2023/6 ([1]) tôi vào topic thảo luận về bài toán đó trên AoPS ([2]) để tham khảo các lời giải khác. Tôi thấy parmenides51 bình luận rằng trong lịch sử IMO thì bài này là bài khó thứ nhì trong các bài hình học, bài khó nhất là bài IMO2011/6. Do tò mò tôi vào trang chủ của IMO ([3]) xem bài toán đó thế nào? Dưới đây là đề bài:

IMO2011/6. Cho tam giác nhọn với đường tròn ngoại tiếp . Giả sử là một tiếp tuyến nào đó của . Gọi , , và là những đường thẳng nhận được từ bằng cách lấy đối xứng qua , , và , tương ứng. Chứng minh rằng đường tròn ngoại tiếp của tam giác tạo bởi ba đường thẳng , , và tiếp xúc với .

Trong điều kiện phòng thi thì thống kê chứng tỏ đây là bài hình học khó nhất trong lịch sử IMO! Ảnh sau tôi lấy từ [3], chỉ có thí sinh làm được bài toán này. Một bài toán rất rất khó!

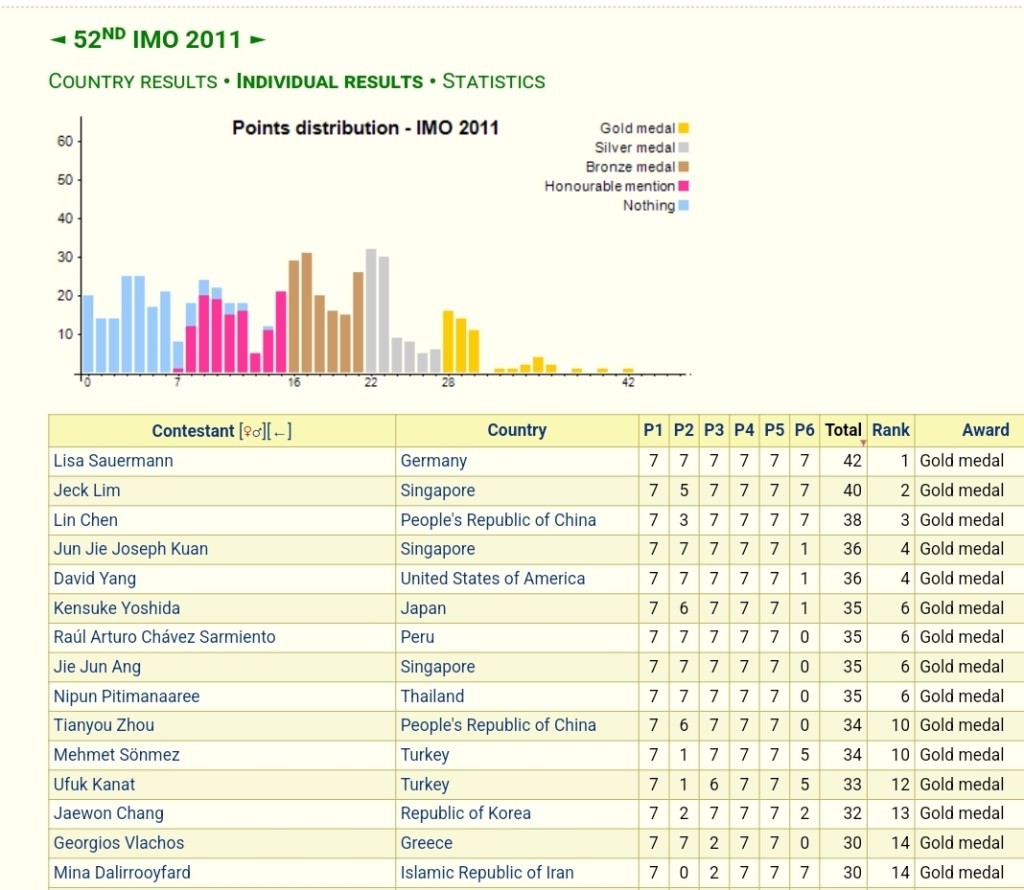
Tôi thích bài IMO2023/6 bởi nó khá lạ so với các bài toán hình thường làm, bài IMO2011/6 này hấp dẫn tôi bởi sự giản dị. Không thể tin được là có kết quả này! Tôi quyết định lập một topic trên blog của tôi để làm việc với bài toán mỗi khi có thời gian (công việc chính của tôi là dạy đại số và số học cho các học sinh Chuyên toán bậc THPT), nó có thể lấy của tôi vài ngày hay nhiều tuần. Khi tôi đang gõ dòng này thì topic đang ở trạng thái ĐỢI, giải được bài toán tôi sẽ bấm nút CÔNG BỐ. Ở mỗi thời điểm, có được kết quả mới nào tôi sẽ sửa vào đây. Lời giải được viết theo hình vẽ trong bài, các trường hợp khác được bỏ qua.

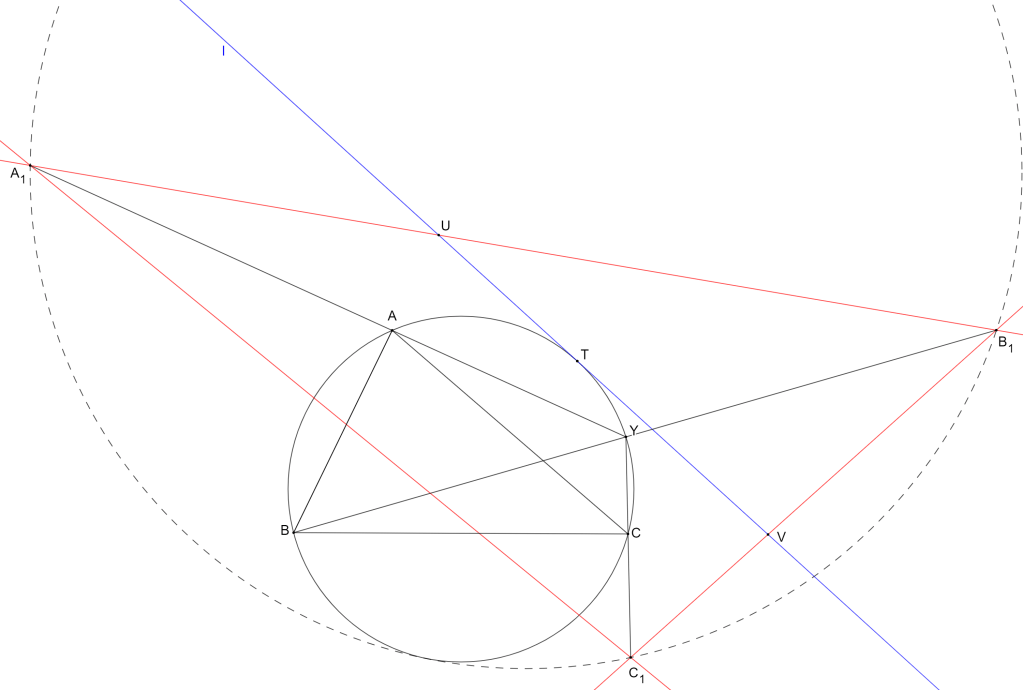
Trong hình vẽ đường thẳng màu xanh là đường thẳng các đường thẳng , , và được tô đỏ.

: Các đường thẳng , và đồng quy. Nếu ký hiệu là điểm chung của ba đường thẳng đó thì là tâm của đường tròn nội tiếp tam giác và nằm trên .

Từ giả thiết ta có và là các phân giác ngoài của tam giác suy ra là phân giác của . Cùng với hai kết quả tương tự ta có các đường thẳng , và đồng quy tại tâm đường tròn nội tiếp của tam giác .

Vì là tâm của đường tròn bàng tiếp tam giác nên ta có

suy ra tứ giác là một tứ giác nội tiếp và ta có . Nói chung, kết quả này vẫn đúng khi là một đường thẳng bất kỳ, không nhất thiết phải là tiếp tuyến của .

Thường thì cái khó của những bài toán kiểu này là không biết đâu là tiếp điểm của hai đường tròn. Việc ta để ý đến các đường thẳng Steiner là hoàn toàn tự nhiên. Khảo sát một lúc chúng tôi giả thuyết là đường thẳng Steiner của tiếp điểm tương ứng với tam giác , trong đó là trực tâm của tam giác còn là điểm chung của và . Từ đây ta tìm được tiếp điểm và có một cách tiếp cận đến bài toán. Nhưng tôi chưa đi theo hướng này! 🙂

Cũng ảnh hưởng bởi các đường thẳng Steiner chúng tôi gọi , , và lần lượt là các điểm đối xứng với qua , , và . Khi đó các điểm này nằm trên một đường thẳng đi qua . Ba đường tròn Miquel , , và cùng đi qua một điểm mà ta ký hiệu là . Rất dễ thấy nằm trên đường tròn . Chúng tôi sẽ chứng minh rằng hai đường tròn và tiếp xúc với nhau tại .

: Điểm nằm trên .

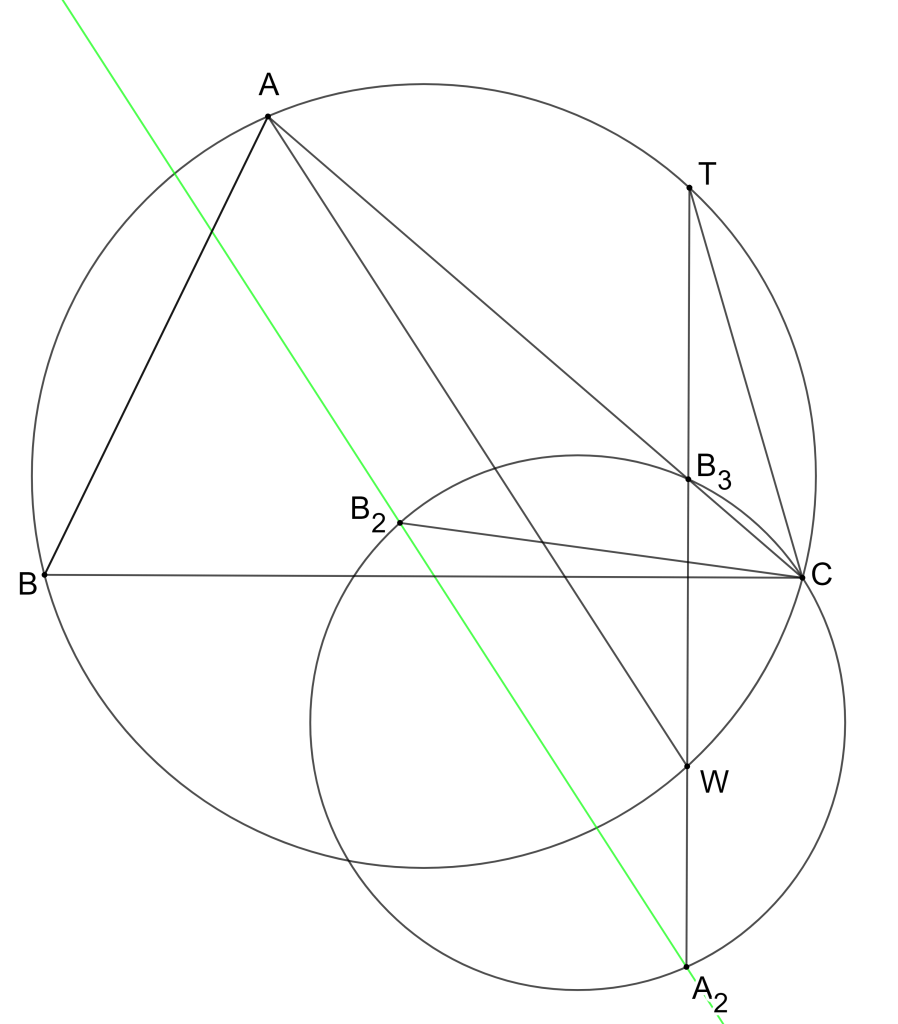
Theo lý thuyết về các đường thẳng Simson ([4]), ta có song song với , suy ra

Nhưng từ ta có , suy ra tứ giác là một tứ giác nội tiếp. Lập luận vừa rồi cũng chứng tỏ nằm trên đường tròn ngoại tiếp tứ giác này.

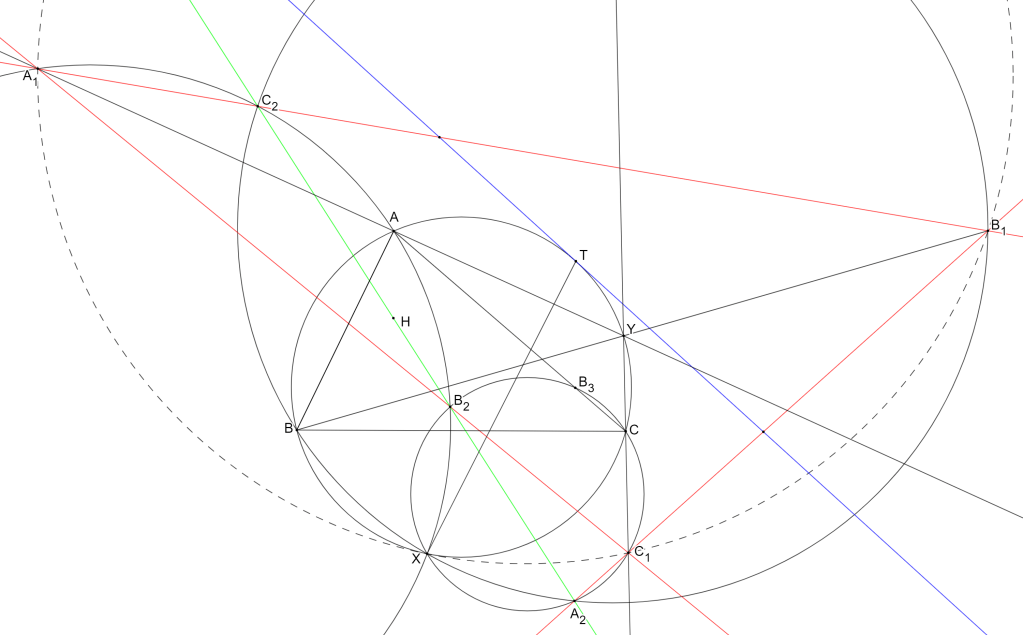
Chứng minh tương tự ta được điểm cùng thuộc một đường tròn.

Bây giờ ta có

Như vậy được chứng minh. Nói chung, kết quả này vẫn đúng khi là một đường thẳng bất kỳ đi qua một điểm trên , không nhất thiết phải là tiếp tuyến của . Lời giải của bài toán này đang ở rất gần tôi, hôm nay tạm thế đã! 🙂

Tiếp tục nào! Như chúng tôi đã nói ở trên, ta chưa dùng giả thiết là tiếp tuyến của . Bây giờ ta sẽ dùng nó!

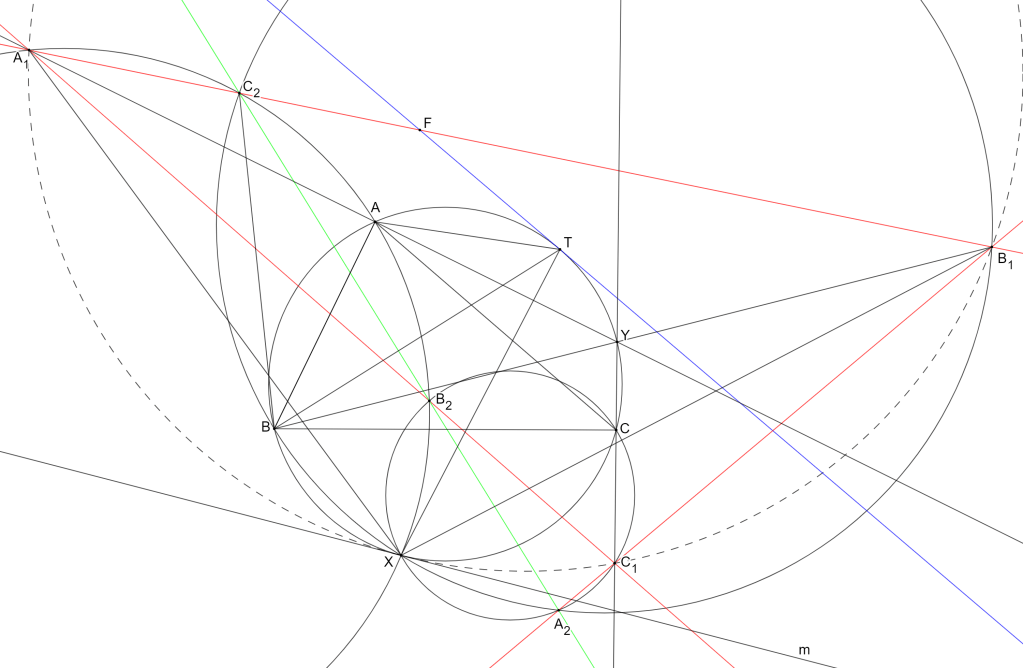
Gọi là tiếp tuyến của đường tròn .

Ta có

, suy ra

Mặt khác, tính toán đơn giản ta được

Do đó , và bởi vậy, cũng là tiếp tuyến của . Bài toán được giải.

Tài liệu tham khảo

[1] https://nttuan.org/2023/07/10/imo2023p6/

[2] https://artofproblemsolving.com/community/c6h3107345

[3] https://www.imo-official.org/

[4] Constantin Mihalescu, The geometry of remarkable elements.

---

Các em học sinh đọc lại toàn bài và loại những chỗ thừa để có lời giải hoàn hảo nhé!