Chúng tôi trình bày lời giải theo hình vẽ tương ứng, các tình huống khác được bỏ qua. Đầu tiên ta phải hiểu thêm về đẳng thức giữa các góc trong đề bài, bởi vì ta không thể vẽ các điểm , và một cách tùy tiện và hy vọng giải được bài toán. Gọi là tâm của tam giác đều . Từ giả thiết ta có suy ra Đến đây ta ký hiệu là ảnh của qua phép quay tâm góc cùng phép quay biến thành .
Khi đó thuộc tia và được viết lại dưới dạng Do đó bốn điểm , , , và cùng nằm trên một đường tròn. Đường tròn này có tâm là vì Như vậy ta đã chứng minh được kết quả sau:
: là tâm của , là tâm của , và là tâm của .
Tiếp theo, ta sẽ tìm hai điểm khác nhau có cùng phương tích đối với cả ba đường tròn ngoại tiếp các tam giác và . Làm được điều này là ta giải được bài toán. Mới đầu chúng tôi định giải nghĩa một cách hình học hai giao điểm của ba đường tròn, hay là chứng minh tâm của ba đường tròn thẳng hàng. Nhưng không thành công!
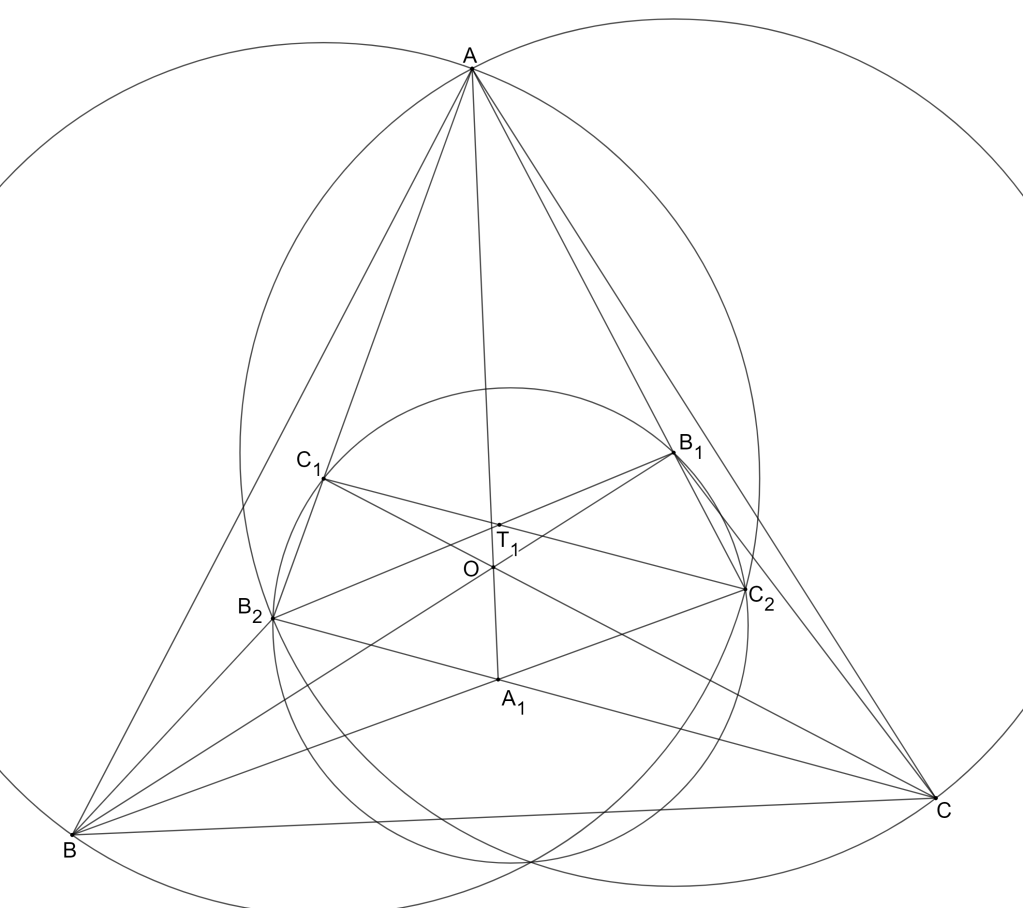
: Ba đường thẳng , , và đồng quy. Nếu ký hiệu là điểm thuộc cả ba đường thẳng, thì có cùng phương tích đối với , , và .
Theo , các tam giác và là các tam giác cân, suy ra Do đó tứ giác là một tứ giác nội tiếp, tương tự ta cũng có hai tứ giác nội tiếp khác. Theo định lí về tâm đẳng phương của ba đường tròn ta có .
:
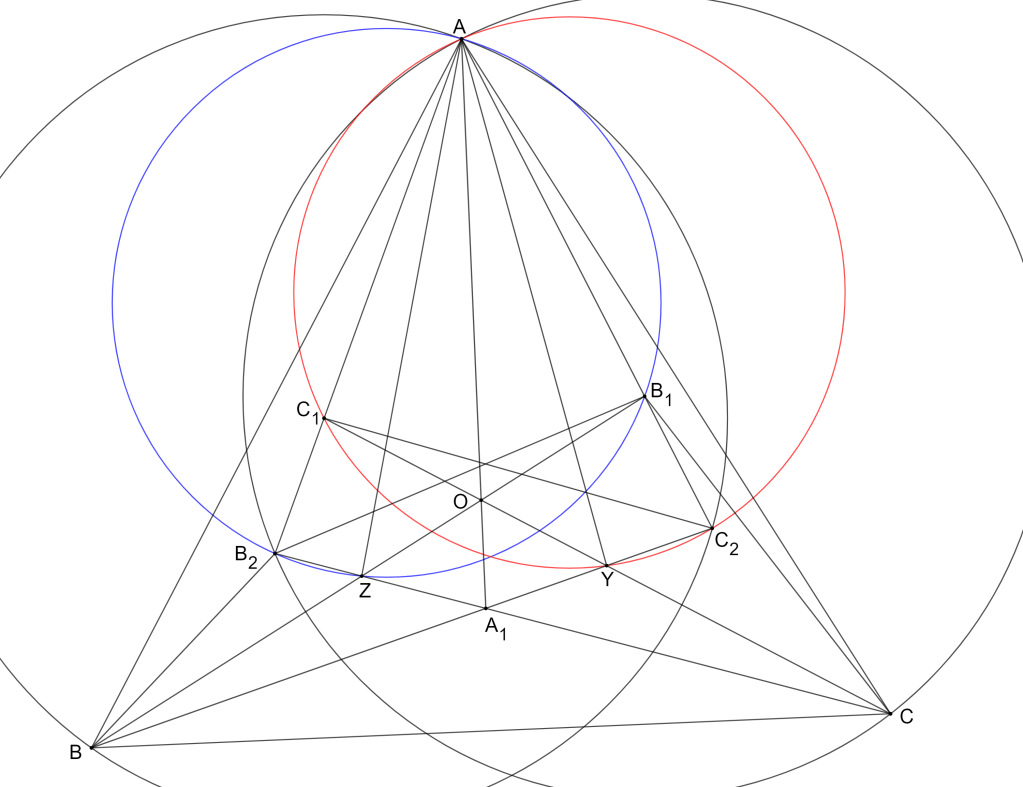
Gọi là giao điểm của với , và là giao điểm của với . Ta có nên tứ giác là một tứ giác nội tiếp. Chứng minh tương tự ta cũng có tứ giác nội tiếp. Từ hai tứ giác nội tiếp này ta thấy vế trái và vế phải trong lần lượt bằng và chỉ việc để ý thêm rằng và đối xứng với nhau qua là ta có .
Bây giờ gọi là giao điểm thứ hai của với , là giao điểm thứ hai của với , và là giao điểm thứ hai của với .
: Ba đường thẳng , , và đồng quy. Nếu ký hiệu là điểm thuộc cả ba đường thẳng, thì có cùng phương tích đối với , , và .
Tính toán đơn giản ta được và Kết hợp với ta có suy ra tứ giác là một tứ giác nội tiếp. Ta cũng có hai tứ giác tương tự nội tiếp. Theo định lí về tâm đẳng phương của ba đường tròn ta có .
T's Lab 
One thought on “IMO2023/6: Coaxal circles”