July 8, 2023 – T's Lab

Bài viết này có hai phần: Phần thứ nhất là đề thi IMO 2023, phần thứ hai là kết qủa của kỳ thi.

Ngày thi thứ nhất, 8/7/2023

Bài 1. https://artofproblemsolving.com/community/c6h3106752

Tìm tất cả các hợp số $n$ có tính chất: nếu $d_1, d_2, \ldots, d_k$ là tất cả ước dương của $n$ với $1=d_1<d_2<\cdots<d_k=n$ , thì $d_i$ chia hết $d_{i+1}+d_{i+2}$ với mọi $1 \leqslant i \leqslant k-2$ .

Bài 2. https://artofproblemsolving.com/community/c6h3106748

Cho tam giác nhọn $ABC$ với $AB<AC$ . Gọi $S$ là điểm chính giữa của cung $BC$ chứa $A$ của $(ABC)$ . Đường thẳng qua $A$ vuông góc với $BC$ cắt $BS$ tại $D$ và cắt lại $(ABC)$ tại $E$ . Đường thẳng qua $D$ song song với $BC$ cắt $BE$ tại $L$ . $(BDL)$ cắt lại $(ABC)$ tại $P$ . Chứng minh rằng tiếp tuyến của $(BDL)$ tại $P$ cắt $BS$ trên phân giác của góc $BAC$ .

Bài 3. https://artofproblemsolving.com/community/c6h3106754

Với số nguyên $k>1,$ tìm tất cả các dãy vô hạn số nguyên dương $a_1,a_2,\ldots$ sao cho tồn tại đa thức $P$ với hệ số nguyên không âm có dạng $P(x)=x^k+c_{k-1}x^{k-1}+\cdots+c_1x+c_0$ để $P(a_n)=a_{n+1}a_{n+2}\cdots a_{n+k}$ với mọi số nguyên dương $n.$

Ngày thi thứ hai, 9/7/2023

Bài 4. https://artofproblemsolving.com/community/c6h3107339

Cho $2023$ số thực dương $x_1,x_2,\ldots,x_{2023}$ đôi một khác nhau thỏa mãn

$\displaystyle a_n=\sqrt{\left(x_1+x_2+\cdots+x_n\right)\left(\frac{1}{x_1}+\frac{1}{x_2}+\cdots+\frac{1}{x_n}\right)}$

là số nguyên với mọi $n=1,2,\ldots,2023$ . Chứng minh rằng $a_{2023}\geq 3034$ .

Bài 5. https://artofproblemsolving.com/community/c6h3107350

Cho $n$ là một số nguyên dương. Một tam giác Nhật Bản gồm $1+2+\cdots+n$ hình tròn được xếp thành một hình tam giác đều sao cho với mỗi $i = 1, 2, ..., n$ , hàng thứ $i$ có đúng $i$ hình tròn và trên hàng đó có đúng một hình tròn được tô màu đỏ. Một đường đi ninja trong một tam giác Nhật Bản là một dãy gồm $n$ hình tròn nhận được bằng cách xuất phát từ hàng trên cùng, đi lần lượt từ một hình tròn xuống một trong hai hình tròn ngay dưới nó, và kết thúc tại hàng dưới cùng. Trong hình vẽ là một tam giác Nhật Bản với $n = 6$ và một đường đi ninja có chứa hai hình tròn màu đỏ.

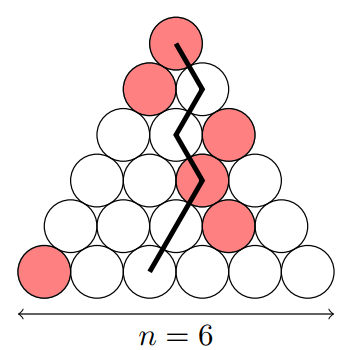
Như một hàm số của $n$ , tìm giá trị lớn nhất của $k$ sao cho trong mỗi tam giác Nhật Bản luôn có một đường đi ninja chứa ít nhất $k$ hình tròn màu đỏ.

Bài 6. https://artofproblemsolving.com/community/c6h3107345

Cho $ABC$ là một tam giác đều. Gọi $A_1,B_1,C_1$ là các điểm nằm trong tam giác $ABC$ sao cho $BA_1=A_1C$ , $CB_1=B_1A$ , $AC_1=C_1B$ , và

$\angle BA_1C+\angle CB_1A+\angle AC_1B=480^\circ.$

Giả sử $BC_1$ và $CB_1$ cắt nhau tại $A_2,$ $CA_1$ và $AC_1$ cắt nhau tại $B_2$ , $AB_1$ và $BA_1$ cắt nhau tại $C_2.$ Chứng minh rằng nếu tam giác $A_1B_1C_1$ là tam giác không cân thì ba đường tròn ngoại tiếp các tam giác $AA_1A_2, BB_1B_2$ và $CC_1C_2$ đi qua hai điểm chung.