Trong bài này tôi giới thiệu nhiều lời giải cho bài toán quan trọng sau:
Bài toán. Cho là các số nguyên không đồng thời bằng
. Chứng minh rằng nếu
là các số nguyên dương đôi một khác nhau và không có ước chính phương lớn hơn
thì
.
Lời giải 1. Ta sẽ chứng minh bằng quy nạp theo , số ước nguyên tố của
, khẳng định: Tồn tại tổng
sao cho
là số nguyên khác
, ở đây
là các số nguyên dương đôi một khác nhau và không có ước chính phương khác
, tập các ước nguyên tố của
là tập con của tập các ước nguyên tố của
,
là các số nguyên, và
. Từ đó suy ra
.
Với ta chọn
.
Với ta chọn
khi
, chọn
nếu
.
Giả sử khẳng định đúng với mọi , ta chứng minh nó đúng với
. Gọi
,
là tất cả các ước nguyên tố của
. Viết
với
,
là các biểu thức cùng dạng với
nhưng không có số nào dưới căn chia hết cho
. Nếu một trong
,
bằng
thì xong, bây giờ ta xét
.
Theo giả thiết quy nạp, tồn tại có dạng như
sao cho
là số nguyên khác
, suy ra
có dạng
, ở đây
có cùng dạng như
. Nhân số này với
ta được
, một số có dạng như
, nếu số này khác
thì theo giả thiết quy nạp, tồn tại tổng
sao cho
là số nguyên khác
. Như vậy
là số nguyên khác
, và khẳng định đúng với
.
Bây giờ ta chỉ ra rằng không thể có . Nếu
là số nguyên thì đương nhiên không thể có, nếu
cũng vậy. Trong trường hợp còn lại, ở dạng thu gọn,
có ít nhất hai căn khác nhau. Không mất tính tổng quát, giả sử
xuất hiện trong một căn nhưng không xuất hiện trong căn kia. Viết
, với
là các biểu thức có dạng như trong khẳng định và các biểu thức dưới dấu căn có ước nguyên tố trong
,
,
,
. Ta có
và
chứa ít nhất
, theo giả thiết quy nạp, số này khác
.
Lời giải 2 (chép từ bình luận của bạn Hopf). Giả sử Xét đa thức
và
đa thức
Đa thức có số mũ của
trong các đơn thức là chẵn vì thay
bởi
thì đa thức không đổi, bởi vậy ta có thể viết
với
và
là các đa thức với hệ số nguyên.
Ta chỉ việc chứng minh không có số nguyên khác là tổ hợp tuyến tính nguyên của các căn, vì khi đó nếu
ta nhân hai vế với
sẽ có mâu thuẫn.
Khẳng định đúng với Giả sử
là số nguyên khác
sao cho
Đa thức có
là một nghiệm nên theo trường hợp
ta có
Do đó suy ra
Từ đây ta thấy
là tổ hợp tuyến tính của các
mâu thuẫn với giả thiết quy nạp.
Lời giải trên mặc dù sơ cấp nhưng rối quá. Dưới đây là một lời giải khác.
Giả sử Xét đa thức
Xét đa thức
 và
và  đa thức
đa thức 
 có số mũ của
có số mũ của  trong các đơn thức là chẵn vì thay
trong các đơn thức là chẵn vì thay 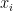 bởi
bởi  thì đa thức không đổi, bởi vậy ta có thể viết
thì đa thức không đổi, bởi vậy ta có thể viết
 với
với 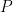 và
và 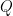 là các đa thức với hệ số nguyên.
là các đa thức với hệ số nguyên.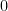 là tổ hợp tuyến tính nguyên của các căn, vì khi đó nếu
là tổ hợp tuyến tính nguyên của các căn, vì khi đó nếu  ta nhân hai vế với
ta nhân hai vế với  sẽ có mâu thuẫn.
sẽ có mâu thuẫn. Giả sử
Giả sử  là số nguyên khác
là số nguyên khác 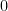 sao cho
sao cho 
 có
có  là một nghiệm nên theo trường hợp
là một nghiệm nên theo trường hợp  ta có
ta có

 suy ra
suy ra  Từ đây ta thấy
Từ đây ta thấy  là tổ hợp tuyến tính của các
là tổ hợp tuyến tính của các 

 mâu thuẫn với giả thiết quy nạp.
mâu thuẫn với giả thiết quy nạp.
Đa thức
Ta chỉ việc chứng minh không có số nguyên khác
Khẳng định đúng với
Đa thức
Do đó