Stern–Brocot tree

Có một dãy tương tự như dãy Farey (xem [1] và [2]), tên chúng là dãy Stern-Brocot. Dãy này được tìm ra một cách độc lập bởi Moritz Stern (1858) và Achille Brocot (1861). Stern là một nhà Toán học Đức còn Brocot là một nhà thiết kế đồng hồ người Pháp.

Trong định nghĩa sau, $\displaystyle \dfrac{1}{0}$ là số hữu tỷ hình thức, ta xem như nó lớn hơn mọi số hữu tỷ. Dãy Stern-Brocot thứ $\displaystyle n\, (n\in\mathbb{N})$ , ký hiệu $\displaystyle SB_n$ , được xác định như sau: $\displaystyle SB_0$ là dãy $\displaystyle \frac{0}{1},\frac{1}{0}$ và với mỗi số nguyên dương $\displaystyle n$ , $\displaystyle SB_n$ được tạo ra bằng cách chép lại toàn bộ (giữ nguyên thứ tự) các số hạng của $\displaystyle SB_{n-1}$ và chèn vào giữa hai số hạng liên tiếp phân số trung gian ở dạng tối giản của chúng.

Một số dãy Stern-Brocot:

$\displaystyle SB_0:\frac{0}{1},\frac{1}{0}$ .

$\displaystyle SB_1:\frac{0}{1},\frac{1}{1},\frac{1}{0}$ .

$\displaystyle SB_2:\frac{0}{1},\frac{1}{2},\frac{1}{1},\frac{2}{1},\frac{1}{0}$ .

Dễ thấy rằng với mỗi số tự nhiên $\displaystyle n$ , $\displaystyle SB_n$ là một dãy tăng gồm $\displaystyle 2^n+1$ số hữu tỷ không âm, và hai số cách đều số ở giữa là nghịch đảo của nhau.

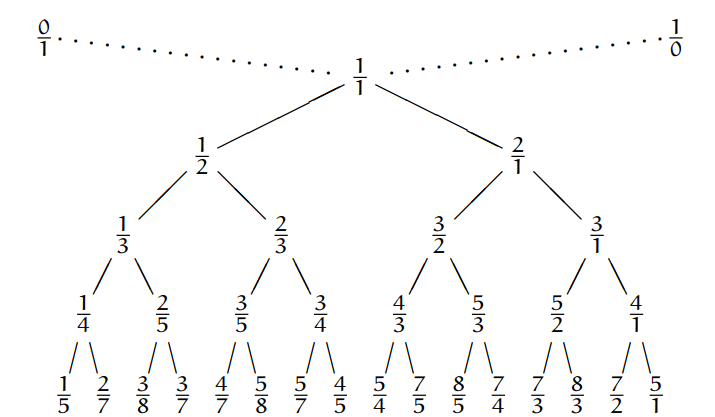
Ta có thể nhúng các dãy Stern-Brocot vào một cây như hình , gọi là cây Stern-Brocot. Ta thấy mỗi số hữu tỷ không âm có mặt đúng một lần trong cây. Thật vậy, vì mỗi dãy Stern-Brocot là một dãy tăng nên mọi số hữu tỷ không âm xuất hiện nhiều nhất một lần trong cây, bây giờ ta chứng minh mọi số hữu tỷ không âm đều xuất hiện trong cây. Xét một số hữu tỷ không âm ở dạng tối giản $\displaystyle \dfrac{m}{n}$ . Tồn tại số tự nhiên $\displaystyle p$ và hai số hạng $\displaystyle \dfrac{a}{b},\dfrac{a'}{b'}$ của $\displaystyle SB_p$ sao cho $\displaystyle \dfrac{a}{b}<\dfrac{m}{n}<\dfrac{a'}{b'}$ . Nếu $\displaystyle \dfrac{m}{n}$ là phân số trung gian của $\displaystyle \dfrac{a}{b},\dfrac{a'}{b'}$ thì tất nhiên nó xuất hiện trong cây, nếu không sẽ xảy ra một trong hai trường hợp: $\displaystyle \dfrac{a}{b}<\dfrac{m}{n}<\dfrac{a+a'}{b+b'}$ , ta thay phân số $\displaystyle \dfrac{a'}{b'}$ bởi $\displaystyle \dfrac{a+a'}{b+b'}$ ; $\displaystyle \dfrac{a+a'}{b+b'}<\dfrac{m}{n}<\dfrac{a'}{b'}$ , ta thay phân số $\displaystyle \dfrac{a}{b}$ bởi $\displaystyle \dfrac{a+a'}{b+b'}$ . Quá trình này không thể tiếp tục mãi vì với dãy dạng $\displaystyle \dfrac{a}{b}<\dfrac{m}{n}<\dfrac{a'}{b'}$ ta luôn có $\displaystyle m+n\geq a+a'+b+b'$ , suy ra $\displaystyle \dfrac{m}{n}$ xuất hiện trong cây.

Khi thay $\displaystyle \dfrac{0}{1}<\dfrac{1}{0}$ bởi hai số hữu tỷ không âm $\displaystyle \dfrac{a}{b}<\dfrac{c}{d}$ với $\displaystyle bc-ad=1$ ta sẽ được các dãy mới, gọi là các dãy Stern-Brocot suy rộng. Có thể chứng minh được rằng mọi số hữu tỷ nằm giữa $\displaystyle \dfrac{a}{b}$ và $\displaystyle \dfrac{c}{d}$ đều xuất hiện trong một dãy Stern-Brocot suy rộng nào đó.